K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 11
đặt x^2+ax+b= (x-1)(x-m)
x^2+ax+b/x^2-1 = x-m/x+1
lim x-m/x+1=-1/2 suy ra 1-m/2=-1/2 nên m = 3
x^2+ax+b= (x-1)(x-3)=x^2-4x+3 suy ra a=-4, b=3
KB
28 tháng 3 2022
Câu 1 : a . \(lim\dfrac{9n^2-3n-1}{7n^3+3n^2}=lim\dfrac{\dfrac{9}{n}-\dfrac{3}{n^2}-\dfrac{1}{n^3}}{7+\dfrac{3}{n}}=0\)
b. \(lim_{x\rightarrow2}\dfrac{\sqrt{4x+1}-3}{4-x^2}=lim_{x\rightarrow2}\dfrac{4x+1-9}{\left(\sqrt{4x+1}+3\right)\left(4-x^2\right)}\)
\(=lim_{x\rightarrow2}\dfrac{4\left(x-2\right)}{\left(\sqrt{4x+1}+3\right)\left(2-x\right)\left(2+x\right)}\)
\(=lim_{x\rightarrow2}\dfrac{-4}{\left(\sqrt{4x+1}+3\right)\left(2+x\right)}=\dfrac{-4}{\left(3+3\right)\left(2+2\right)}=-\dfrac{1}{6}\)
KB
28 tháng 3 2022
Câu 2 : Ta có : f(x) = \(\left\{{}\begin{matrix}2x^2+x\left(x< 2\right)\\mx-1\left(x\ge2\right)\end{matrix}\right.\)
TXĐ : D = R . Với x < 2 ; hàm số liên tục
Với x > 2 ; hàm số liên tục
Với x = 2 , ta có : \(lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^-}2x^2+x=2.2^2+2=10\)
\(lim_{x\rightarrow2^+}f\left(x\right)=lim_{x\rightarrow2^+}mx-1=2m-1\)
Hàm số liên tục trên R <=> Hàm số liên tục tại x = 2
\(\Leftrightarrow lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^+}f\left(x\right)\)
\(\Leftrightarrow10=2m-1\) \(\Leftrightarrow m=\dfrac{11}{2}\)
Vậy ...
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)
5 tháng 4 2023
a: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
b: (SB;(ABCD))=(BS;BA)=góc SBA
\(\sin SBA=\dfrac{SA}{SB}=\dfrac{a\sqrt{3}}{2a}=\dfrac{\sqrt{3}}{2}\)
=>góc SBA=60 độ
TM
Tìm đạo hàm của hàm số \(y=\dfrac{a^3}{\sqrt{a^2-x^2}}\) (a là hằng số)
Giúp mình với ạ, mình cảm ơnn
1
HT
26 tháng 4 2021
\(y'=\dfrac{\left(a^3\right)'.\sqrt{a^2-x^2}-\left(\sqrt{a^2-x^2}\right)'.a^3}{a^2-x^2}=\dfrac{-\dfrac{1}{2\sqrt{a^2-x^2}}\left(a^2-x^2\right)'.a^3}{a^2-x^2}\)
\(y'=\dfrac{x.a^3}{\sqrt{a^2-x^2}\left(a^2-x^2\right)}\)
26 tháng 10 2016
xin lỗi mình chép thiếu đề H là trung điểm AB và SH bằng a và vuông góc với đáy
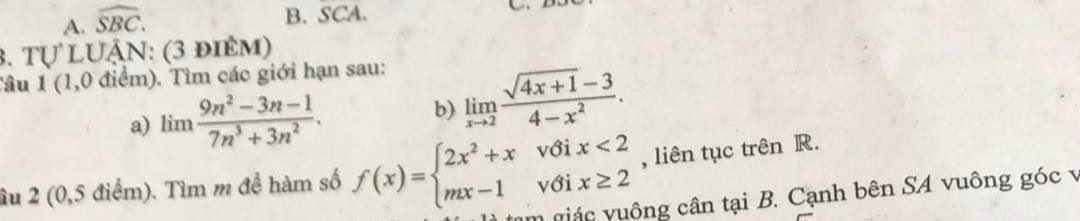
1.
Gọi B là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\)
Theo công thức tọa độ phép tịnh tiến:
\(\left\{{}\begin{matrix}x_B=-4+3=-1\\y_B=-9+\left(-7\right)=-16\end{matrix}\right.\)
\(\Rightarrow B=\left(-1;-16\right)\)
2.
Giả sử \(T_{\overrightarrow{u}}\left(d\right)=d'\Rightarrow d||d'\)
\(\Rightarrow\) Phương trình d' có dạng: \(3x-7y+c=0\) (1)
Lấy \(M\left(-2;0\right)\in d\)
Gọi \(T_{\overrightarrow{u}}\left(M\right)=M'\Rightarrow M'\in d'\)
Theo công thức phép tịnh tiến:
\(\left\{{}\begin{matrix}x_{M'}=-2+10=8\\y_{M'}=0+\left(-3\right)=-3\end{matrix}\right.\)
Thế vào (1) ta được: \(3.8-7.\left(-3\right)+c=0\Rightarrow c=-45\)
Vậy pt d' có dạng: \(3x-7y-45=0\)
3.
Đường tròn (C) có tâm \(I\left(-2;4\right)\) bán kính \(R=4\)
Gọi \(T_{\overrightarrow{v}}\left(C\right)=\left(C'\right)\Rightarrow\left(C'\right)\) là đường tròn có bán kính R và tâm \(I'\left(a';b'\right)\) là ảnh của I qua phép tịnh tiến \(\overrightarrow{v}\)
\(\Rightarrow\left\{{}\begin{matrix}x'=-2+\left(-7\right)=-9\\y'=4+\left(-1\right)=3\end{matrix}\right.\)
\(\Rightarrow I'\left(-9;3\right)\)
Phương trình (C') có dạng:
\(\left(x+9\right)^2+\left(y-3\right)^2=16\)
4.
Đường tròn (C) tâm \(I\left(-1;2\right)\) bán kính \(R=\sqrt{\left(-1\right)^2+2^2-\left(-15\right)}=\sqrt{20}\)
Lý luận tương tự câu trên, ta có:
\(\left\{{}\begin{matrix}x'=-1+\left(-4\right)=-5\\y'=2+5=7\end{matrix}\right.\)
Phương trình (C') có dạng:
\(\left(x+5\right)^2+\left(y-7\right)^2=20\)