Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Kẻ \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow\widehat{ACH}\) là góc giữa AC và (SBC)
\(AC=a\sqrt{2}\) ; \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{1}{\dfrac{6a^2}{9}}+\dfrac{1}{a^2}\Rightarrow AH=\dfrac{a\sqrt{10}}{5}\)
\(\Rightarrow sin\widehat{ACH}=\dfrac{AH}{AC}=\dfrac{\sqrt{5}}{5}\Rightarrow\widehat{ACH}\approx26^034'\)

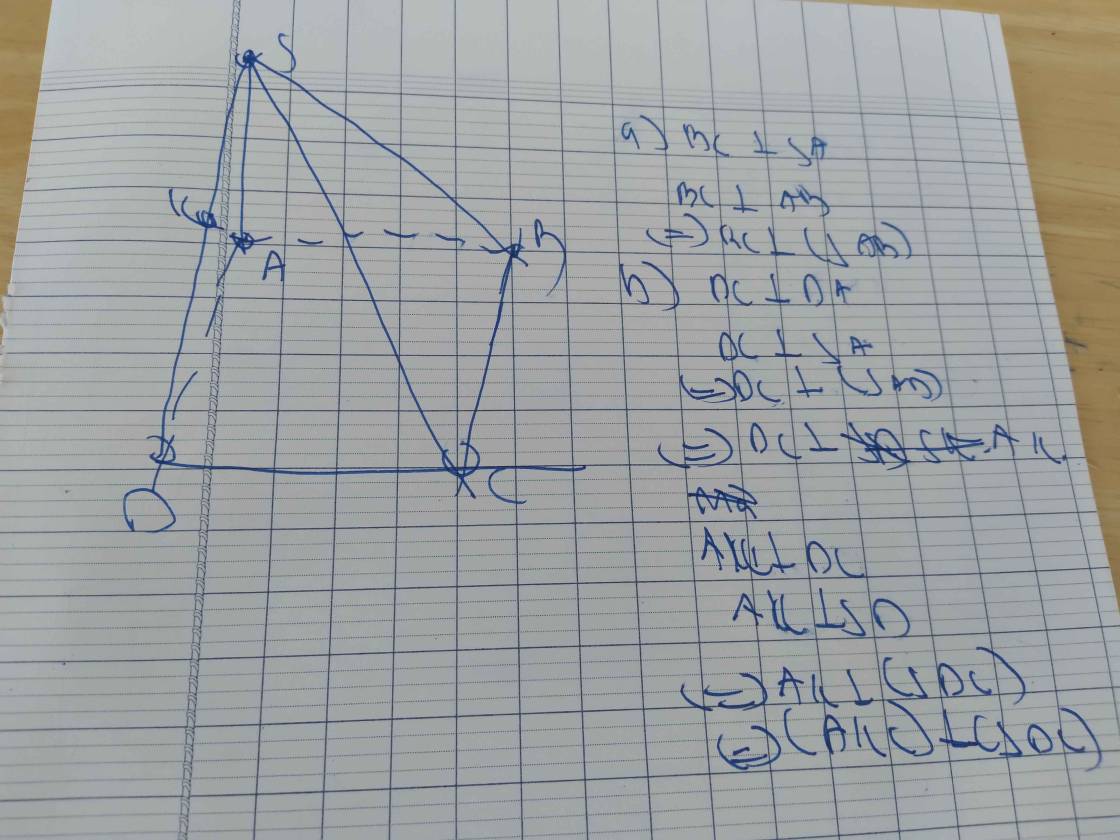
a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ



a: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
b: (SB;(ABCD))=(BS;BA)=góc SBA
\(\sin SBA=\dfrac{SA}{SB}=\dfrac{a\sqrt{3}}{2a}=\dfrac{\sqrt{3}}{2}\)
=>góc SBA=60 độ