
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$x+y=16(1)$
$x,y$ tỉ lệ nghịch với $3,5$ nên $3x=5y\Rightarrow x=\frac{5}{3}y$. Thay vô $(1)$:
$\frac{5}{3}y+y=16$
$\frac{8}{3}y=16$
$y=6$
$\Rightarrow x=\frac{5}{3}y=\frac{5}{3}.6=10$
Vậy $x=10; y=6$


Bài 1:
b: Xét ΔOAC và ΔOBD có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)
OC=OD
Do đó: ΔOAC=ΔOBD
Nếu cậu làm hết thì tớ sẽ thả đúng và một lượt theo dõi:3(không làm cũng không sao tớ cảm ơn)

Bài 1:
a: \(x-\dfrac{3}{7}=\dfrac{2}{3}\)
\(\Leftrightarrow x=\dfrac{2}{3}+\dfrac{3}{7}=\dfrac{14+9}{21}=\dfrac{23}{21}\)


Tg ABC cân
=> AB=AC (1)
AN=BN (gt) (2); AM=CM (gt) (3)
Xét tg ABM và tg ACN có
\(\widehat{A}\) chung
AB=AC
Từ (1) (2) (3)
\(\Rightarrow AN=AM\)
=> tg ABM = tg ACN (c.g.c) => BM=CN
b/
Ta có G là trong tâm của tg ABC
\(\Rightarrow GM=\dfrac{1}{3}BM\Rightarrow GM=\dfrac{1}{2}BG\Rightarrow BG=2.GM\)
\(\Rightarrow GN=\dfrac{1}{3}CN\Rightarrow GN=\dfrac{1}{2}CG\)
Mà BM=CN (cmt) => GM=GN => BG = CG = 2.GM
Xét tg BGC có
\(BC< BG+CG\) (trong tg dộ dài 1 cạnh nhỏ hơn tổng độ dài 2 cạnh còn lại)
\(\Rightarrow BG+CG>BC\Rightarrow4.GM>BC\Rightarrow GM>\dfrac{1}{4}BC\)


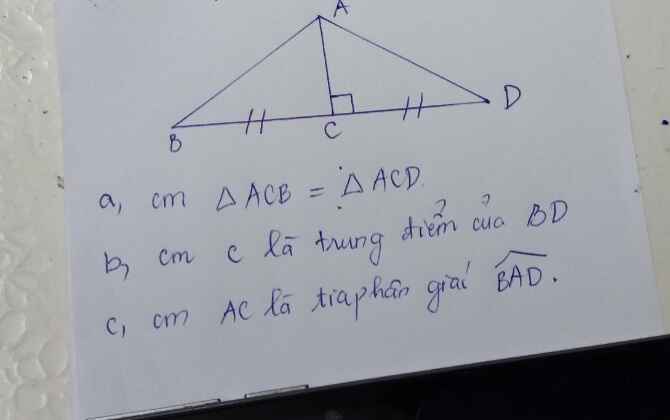 giúp tớ với, tớ đang cần gấp ạ.
giúp tớ với, tớ đang cần gấp ạ.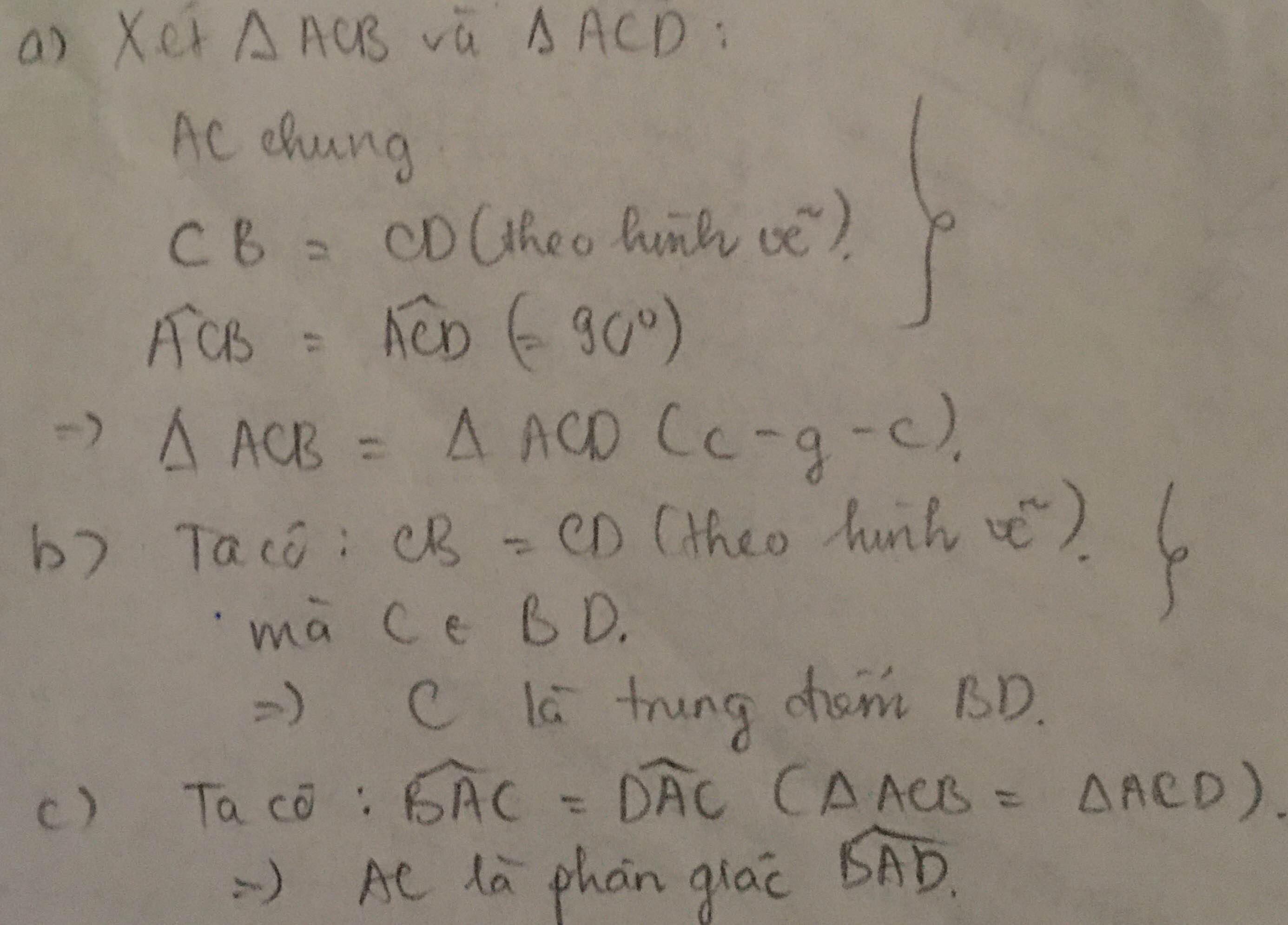

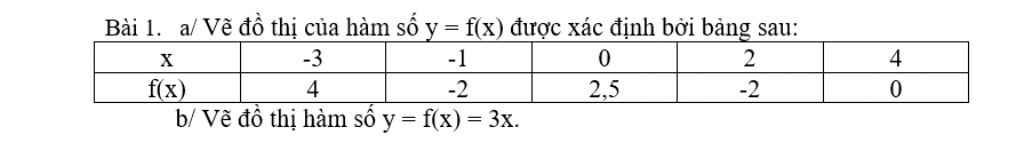
 giúp tớ bài này với ạ:3 tớ đang cần gấp
giúp tớ bài này với ạ:3 tớ đang cần gấp



a) \(M\left(x\right)=0\Rightarrow3x-7=0\Rightarrow x=\dfrac{7}{3}\)
Vậy \(x=\dfrac{7}{3}\) là nghiệm của đa thức đã cho.
b) \(N\left(x\right)=0\Rightarrow x^3+2x=0\Rightarrow x\left(x^2+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2+2=0\left(L\right)\end{matrix}\right.\)
Vậy \(x=0\) là nghiệm của đa thức đã cho.
Xét 3x-7=0 có:
3x-7=0
3x=7
x=7/3
vậy x=7/3.