
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x^3-3\left|y+1\right|=18\\2x^3+3\left|y+1\right|=22\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x^3=40\\2x^3+3\left|y+1\right|=22\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^3=8\\2x^3+3\left|y+1\right|=22\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^3=8\\\left|y+1\right|=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\end{matrix}\right.\)

Bài 1:
a: Xét tứ giác NPIK có
\(\widehat{NKP}=\widehat{NIP}\left(=90^0\right)\)
Do đó: NPIK là tứ giác nội tiếp
hay N,P,I,K cùng thuộc 1 đường tròn
b: Xét tứ giác MKHI có
\(\widehat{MKH}+\widehat{MIH}=180^0\)
Do đó: MKHI là tứ giác nội tiếp
hay M,K,H,I cùng thuộc 1 đường tròn

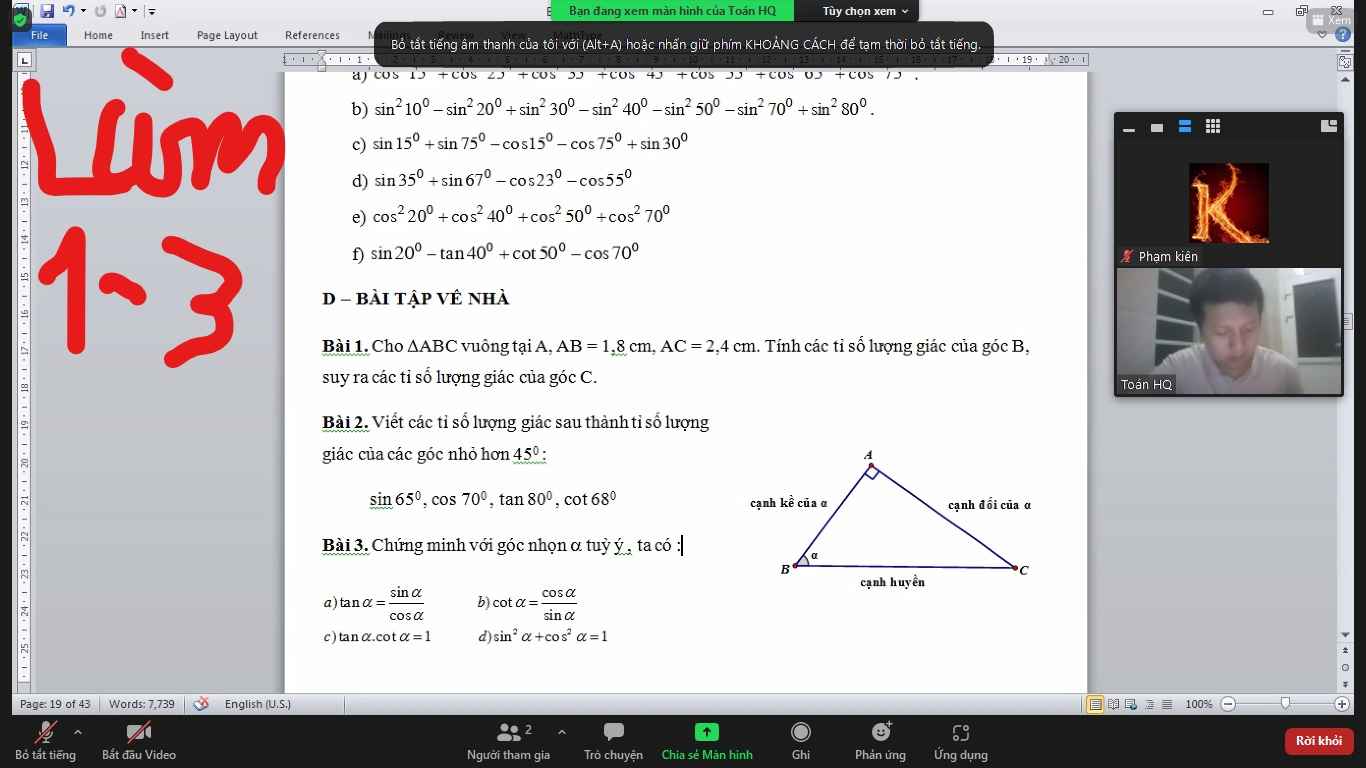
sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)

Ta có:
\(\Delta=b^2-4ac=\left(-m\right)^2-4.2.m\) \(=m^2-8m\)
Để phương trình có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow m^2-8m\ge0\Leftrightarrow\left[{}\begin{matrix}m\le0\\m\ge8\end{matrix}\right.\)

a: Gọi (d):y=ax+b là phương trình đường thẳng đi qua hai điểm M và N
(d) đi qua M(3;-1) nên thay x=3 và y=-1 vào (d), ta được:
3a+b=-1
(d) đi qua N(-2;-2) nên thay x=-2 và y=-2 vào (d), ta được:
-2a+b=-2
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-1\\-2a+b=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5a=1\\3a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{5}\\b=-1-3a=-1-\dfrac{3}{5}=-\dfrac{8}{5}\end{matrix}\right.\)
=>(d): \(y=\dfrac{1}{5}x-\dfrac{8}{5}\)
c: Gọi (d): y=ax+b là phương trình đường thẳng đi qua hai điểm P,Q
(d) đi qua P(2;3) nên thay x=2 và y=3 vào (d), ta được:
2a+b=3
(d) đi qua Q(-2;-1) nên thay x=-2 và y=-1 vào (d), ta được:
-2a+b=-1
Do đó, ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=3\\-2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2b=2\\2a+b=3\end{matrix}\right.\)
=>b=1 và 2a=3-b=2
=>b=1 và a=1
=>(d): y=x+1
 Giúp mk mấy bài này vs ạ
Giúp mk mấy bài này vs ạ
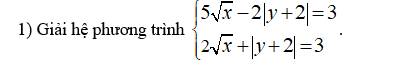

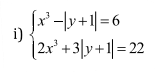


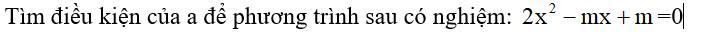
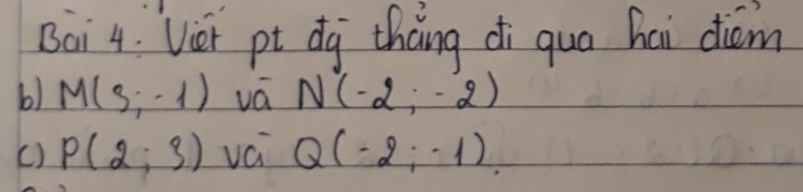
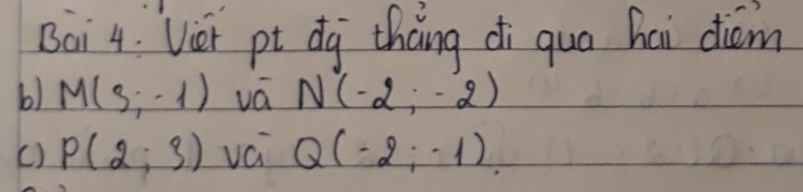
1:
4:
a: \(B=\dfrac{x-x+\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
Khi x=9/25 thì B=3/5:(3/5-1)=3/5:(-2/5)=-3/2
b: \(A=\dfrac{x-1+\sqrt{x}+2-x}{x-\sqrt{x}}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}}\)
c: P=B:A
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}+1}=\dfrac{x}{\sqrt{x}+1}\)
P nguyên
=>x-1+1 chia hết cho căn x+1
=>căn x+1 thuộc Ư(1)
=>căn x+1=1 hoặc căn x+1=-1
=>căn x=-2(loại) hoặc căn x=0(loại)