K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 5 2016
\(\sqrt{x^2-4x+49}-49=0\Leftrightarrow x^2-4x+49=49^2\Leftrightarrow x^2-4x-2352=0\)
Den day ban tu giai!
TY
4
MT
18 tháng 7 2016
Đặt a=x2+x+2>0, phương trình trên trở thành:
\(\sqrt{a+5}+\sqrt{a}=\sqrt{3a+13}\)
\(\Rightarrow2a+5+2\sqrt{a^2+5a}=3a+13\)
\(\Leftrightarrow2\sqrt{a^2+5a}=a+8\)
\(\Leftrightarrow4a^2+20a=a^2+16a+64\)
\(\Leftrightarrow3a^2+4a-64=0\)
\(\Delta=784>0\Rightarrow\sqrt{\Delta}=28\)
=>PT có 2 nghiệm phân biệt: \(a_1=4\)(nhận);\(a_2=-\frac{16}{3}\)(loại)
Do đó : \(x^2+x+2=4\Leftrightarrow x^2+x-2=0\)
Ta có : a+b+c=1+1-2=0
=>phương trình có 2 nghiệm pb: \(x_1=1;x_2=-2\)
Vậy tập nghiệm của PT là: S={1;-2}
HP
12 tháng 9 2021
1.
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
HP
12 tháng 9 2021
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)
HP
4 tháng 3 2022
a. \(\Delta'=1^2-1.\left(-3\right)=4>0\)
Do \(\Delta'>0\) nên PT luôn có 2 nghiệm phân biệt.
b. Dựa vào hệ thức Vi - ét, ta có:
\(\left\{{}\begin{matrix}S=x_1+x_2=-\dfrac{b}{a}=-\dfrac{2}{1}=-2\\P=x_1x_2=\dfrac{c}{a}=-\dfrac{3}{1}=-3\end{matrix}\right.\)
c. \(U=\left(x_2-x_2\right)^2-2x_1^2x_2^2\)
\(=x_1^2-2x_1x_2+x_2^2-2\left(x_1x_2\right)^2\)
\(=x_1^2+x^2_2-2x_1x_2-2\left(x_1x_2\right)^2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2-2\left(x_1x_2\right)^2\)
\(=\left(-2\right)^2-2.\left(-3\right)-2.\left(-3\right)^2\)
\(=-8\)
d. \(A=\dfrac{1}{x_1}+\dfrac{1}{x_2}-3\)
\(=\dfrac{x_2}{x_1x_2}+\dfrac{x_1}{x_1x_2}-3\)
\(=\dfrac{x_1+x_2}{x_1x_2}-3\)
\(=\dfrac{-2}{-3}-3\)
\(=-\dfrac{7}{3}\)
27 tháng 6 2021
`D=(sqrt{3}.sqrt{5-2sqrt6})/(sqrt3-sqrt2)-1/(2-sqrt3)`
`=(sqrt3*sqrt{3-2sqrt{3}.sqrt2+2})/(sqrt3-sqrt2)-(2+sqrt3)/(4-3)`
`=(sqrt3.sqrt{(sqrt3-sqrt2)^2})/(sqrt3-sqrt2)-2-sqrt3`
`=sqrt3-2-sqrt3=-2`
18 tháng 9 2023
a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)
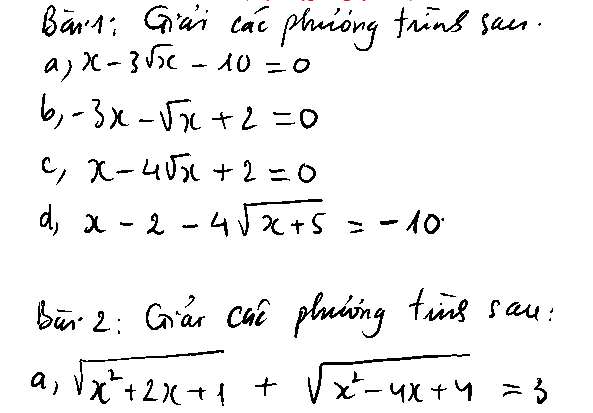
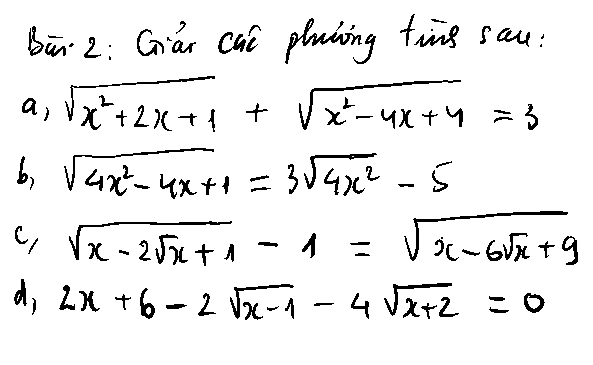
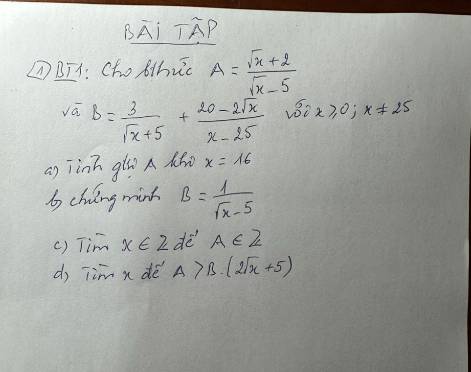
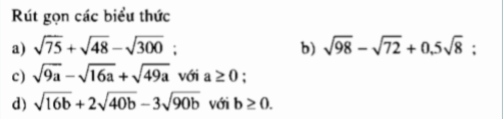
Giải giúp em câu d
`d)sqrt{7-2sqrt{10}}-sqrt{7+2sqrt{10}}`
`=sqrt{5-2sqrt{5}.sqrt2+2}-sqrt{5+2sqrt{5}.sqrt2+2}`
`=sqrt{(sqrt5-sqrt2)^2}-sqrt{(sqrt5+sqrt2)^2}`
`=sqrt5-sqrt2-sqrt5-sqrt2=-2sqrt2`
d, \(\sqrt{7-2\sqrt{10}}-\sqrt{7+2\sqrt{10}}=\sqrt{5-2.\sqrt{2}.\sqrt{5}+2}-\sqrt{5+2.\sqrt{2}.\sqrt{5}+2}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{2}\right)^2}=\left|\sqrt{5}-\sqrt{2}\right|-\left|\sqrt{5}+\sqrt{2}\right|\)
\(=\sqrt{5}-\sqrt{2}-\sqrt{5}-\sqrt{2}=-2\sqrt{2}\)