K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
6 tháng 9 2021
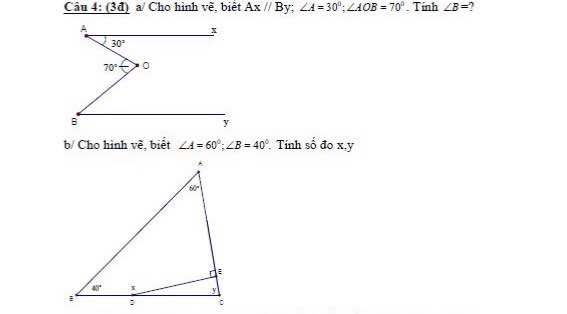
Câu 4a.
Kẻ tia $Om\parallel Ax$ như hình:
Vì $Ax\parallel Om$ nên $\widehat{AOm}=\widehat{xAO}=30^0$ (hai góc so le trong)
$\Rightarrow \widehat{mOB}=\widehat{AOB}-\widehat{AOm}=70^0-30^0=40^0$
$Ax\parallel By, Ax\parallel Om\Rightarrow By\parallel Om$
$\Rightarrow \widehat{B}=\widehat{mOB}=40^0$ (hai góc so le trong)
6 tháng 9 2021
a) Trên nửa mặt phẳng bờ OB chứa điểm A, kẻ tia Oz//Ax//By
Ta có: Oz//Ax(cách vẽ)
\(\Rightarrow\widehat{xAO}=\widehat{AOz}=30^0\)( 2 góc so le trong)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{zOB}=\widehat{AOB}-\widehat{AOz}=70^0-30^0=40^0\)
Ta có: Oz//By
\(\Rightarrow\widehat{B}=\widehat{zOB}=40^0\)( 2 góc so le trong)
b) Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
\(\Rightarrow y=80^0\)
Xét tứ giác AEDB có:
\(\widehat{AED}+\widehat{EDB}+\widehat{ABD}+\widehat{BAE}=360^0\)
\(\Rightarrow\widehat{EDB}=360^0-\widehat{AED}-\widehat{ABD}-\widehat{BAE}=360^0-90^0-40^0-60^0=170^0\)
\(\Rightarrow x=170^0\)
26 tháng 3 2022
có: tam giác ABO cân tại A (gt)
=> AB=AO (tính chất tam giác cân)
Có: AH vuông góc BO (gt)
=> góc AHB = góc AHO (tính chất đường vuông góc)
Xét tam giác AHB và tam giác AHO có
goc AHB = góc AHO (cmt)
AB = AO (cmt)
AH chung
=> tam giác AHB = tam giác AHO (cạnh huyền - cạnh góc vuông)
TI
12 tháng 7 2018
a)Tam giác BAE có BE=BA (gt)
=> tam giác BAE cân tại B
=>góc BEA=góc BAE
Mà góc AEK=góc BAE
=>góc BEA=góc AEK
Vậy EA là pgiac của góc BEK
b) Tam giác AHE vuông tại H và tam giác AKE vuông tại K có:
AE là cạnh chung
góc HEA=góc KEA(cmt)
=>tam giác AHE-=tam giác AKE (c.huyền-g.nhọn)
=>AH=AK
VM
12 tháng 7 2018
a) Ta có EK \(\perp\)AC (gt)
Mà AB \(\perp\)AC (tam giác ABC vuông tại A)
=> EK // AB
Nên \(\widehat{BAE}\)=\(\widehat{AEK}\)(1)
Ta lại có AB = BE
=> Tam giác ABE cân tại B
Nên \(\widehat{BAE}\)= \(\widehat{AEB}\)(2)
Từ (1) và (2) => \(\widehat{AEB}\)= \(\widehat{AEK}\)
Hay EA là phân giác của góc BEK
b) Xét tam giác vuông AHE và tam giác vuông AKE có
AE: cạnh chung
\(\widehat{AEB}=\widehat{AEK}\)
=> Tam giác vuông AHE = tam giác vuông AKE (ch-gn)
=>AK = AH (đpcm)
14 tháng 1
Bài 3:
a: \(Q=A\cdot B\)
\(=\dfrac{-2}{5}x^3yz^2\cdot\dfrac{1}{2}\cdot x^2y^3z\)
\(=\left(-\dfrac{2}{5}\cdot\dfrac{1}{2}\right)\cdot\left(x^3\cdot x^2\right)\cdot\left(y\cdot y^3\right)\left(z^2\cdot z\right)\)
\(=\dfrac{-1}{5}\cdot x^5y^4z^3\)
b: \(Q=\dfrac{-1}{5}x^5y^4z^3\)
Hệ số là \(-\dfrac{1}{5}\)
Phần biến là \(x^5;y^4;z^3\)
bậc là 5+4+3=12
Bài 1:
Thay x=1/2 và y=-1 vào \(M=3xy^3+\dfrac{1}{2}-2xy^2\), ta được:
\(M=3\cdot\dfrac{1}{2}\cdot\left(-1\right)^3+\dfrac{1}{2}-2\cdot\dfrac{1}{2}\cdot\left(-1\right)^2\)
\(=-\dfrac{3}{2}+\dfrac{1}{2}-1\)
=-1-1
=-2
VA
3
4 tháng 5 2021
a) Xét t/giấc OHA và t/giác OMA có
OHA=OMA (90 độ)
HOA=MOA(OA là tia pg của MOH)
OA là cạnh chung
Do đó t/giác OHA= t/giác OMA(chgn)
suy ra OH=OM(2 cạnh t/ứ)
b) Vì t/giác OHA vuông tại H
suy ra \(HA^2\)+\(OH^2\)=\(OA^2\) (ĐL PY TA GO)
\(5^2\)+\(OH^2\)=\(13^2\)
25+\(OH^2\)=169
\(OH^2\)=144
OH=12 cm
Mà OH=OM(cmt)
Suy ra OM=12 cm
chúc bạn học tốt :D
YU
3
5 tháng 1 2022
a: \(=\dfrac{10}{7}-\dfrac{10}{7}+\dfrac{1}{4}=\dfrac{1}{4}\)
b: \(=\dfrac{6}{5}\left(\dfrac{19}{11}+\dfrac{36}{11}\right)=\dfrac{6}{5}\cdot5=6\)
c: \(=3\cdot\dfrac{1}{4}-6=\dfrac{3}{4}-\dfrac{24}{4}=-\dfrac{21}{4}\)
Giúp mình với mình đang gấp lắm ạ!