Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tgiac ABH và ACH đều vuông ở H
Do tổng 3 góc trong 1 tgiac là 180o nên ta có: góc B + HAB = C + HAC = 90o (1)
Xét tgiac ABC có AB < AC => góc C < góc B (2)
(1), (2) => góc HAC > HAB
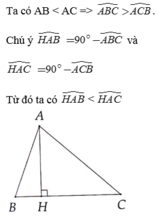
Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ AH vuông góc với BC tại H. So sánh H A B ^ và H A C ^ .


hình e tự vẽ nhé
a) Xét tam giác BHA vuông tại H có
góc B + góc HAB = 90 độ ( hai góc phụ nhau)
40 độ + góc HAB = 90 độ
=> góc HAB = 50 độ
mà góc HAB + góc HAC = 90 độ ( tam giác ABC có góc A = 90 độ)
Ta lại có góc HAC + Góc C = 90 độ ( hai góc phụ nhau )
=> góc HAB = góc C = 50 độ

a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
\(\Leftrightarrow\widehat{C}=90^0-40^0=50^0\)

Bạn vào ô công thức để nhập lại số đo góc đi bạn. Khó hiểu quá

AB<AC
=>góc B>góc C
=>90 độ-góc B<90 độ-góc C
=>góc HAB<góc HAC

có cần vẽ hình ko bn