
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
$A=(-2x^3+6x^3)+(6x^3y-25x^3y)+(7y+8y)-20$
$=4x^3-19x^3y+15y-20$
b.
$B=(5x^3-14x^3)+(9xy^4-13xy^4)-3y^2+(17-23)$
$=-9x^3-4xy^4-3y^2-6$
b.
Bậc của $A$ gắn với $-19x^3y$, là $3+1=4$
Bậc của $B$ gắn với $-4xy^4$, là $1+4=5$
ab, \(A=-2x^3-19x^3y+15y-20\)
-> bậc 4
\(B=-9x^3-4xy^4-3y^2-5\)
-> bậc 5

b: Ta có: 2x=3y=5z
\(\Leftrightarrow\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{5}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{5}}=\dfrac{x-2y+z}{\dfrac{1}{2}-\dfrac{2}{3}+\dfrac{1}{5}}=\dfrac{14}{\dfrac{1}{30}}=420\)
Do đó: x=210; y=140; z=84

a) \(\left|x\right|=3\dfrac{1}{2}\)
\(\Rightarrow\left|x\right|=\dfrac{7}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
b) \(\left|x-1,2\right|=2,8\)
\(\Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-1,6\end{matrix}\right.\)
\(a,\left|x\right|=3\dfrac{1}{2}\)
\(\Rightarrow x=\left[{}\begin{matrix}3\dfrac{1}{2}\\-3\dfrac{1}{2}\end{matrix}\right.\)
\(b,\left|x-1,2\right|=2,8\\ \Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2,8+1,2=4\\x=-2,8+1,2=-1,6\end{matrix}\right.\)
Vậy \(x\in\left\{4;-1,6\right\}\)


Câu 1:
\(\sqrt{16}=4\)
\(\sqrt{36}=6\)
\(\sqrt{81}=9\)
\(\sqrt{144}=12\)
\(\sqrt{625}=25\)
\(\sqrt{\dfrac{4}{9}}=\dfrac{2}{3}\)
\(\sqrt{\dfrac{36}{25}}=\dfrac{6}{5}\)
\(\sqrt{\dfrac{64}{49}}=\dfrac{8}{7}\)
\(\sqrt{\dfrac{169}{400}}=\dfrac{13}{20}\)
\(\sqrt{11\dfrac{1}{9}}=\sqrt{\dfrac{100}{9}}=\dfrac{10}{3}\)
\(\sqrt{1\dfrac{11}{25}}=\sqrt{\dfrac{36}{25}}=\dfrac{6}{5}\)
\(\sqrt{1\dfrac{13}{36}}=\sqrt{\dfrac{49}{36}}=\dfrac{7}{6}\)
Câu 2:
a) \(3.\sqrt{16}-4\sqrt{\dfrac{1}{4}}\)
\(=3.4-4.\dfrac{1}{2}\)
\(=4.\left(3-\dfrac{1}{2}\right)\)
\(=4.\dfrac{5}{2}\)
\(=10\)
b) \(-5\sqrt{\dfrac{9}{16}}+4\sqrt{0,36}-6\sqrt{0,09}\)
\(=-5.\dfrac{3}{4}+4.0,6-6.0,3\)
\(=\dfrac{-15}{4}+\dfrac{12}{5}-\dfrac{9}{5}\)
\(=\dfrac{-75+48-36}{20}=\dfrac{-63}{20}\)
c) \(2.\sqrt{9}-10.\sqrt{\dfrac{1}{25}}\)
\(=2.3-10.\dfrac{1}{5}\)
\(=6-2\)
\(=4\)
d) \(-3\sqrt{\dfrac{25}{16}}+5\sqrt{0,16}-7\sqrt{0,64}\)
\(=-3.\dfrac{5}{4}+5.0,4-7.0,8\)
\(=\dfrac{-15}{4}+2-\dfrac{28}{5}\)
\(=\dfrac{-75+40-28}{20}=\dfrac{-63}{20}\)
e) \(3\sqrt{25}-27\sqrt{\dfrac{4}{81}}\)
\(=3.5-27.\dfrac{2}{9}\)
\(=15-6\)
\(=9\)
f) \(-21\sqrt{\dfrac{100}{49}}+3\sqrt{0,04}-5\sqrt{0,25}\)
\(=-21.\dfrac{10}{7}+3.0,2-5.0,5\)
\(=-30+\dfrac{3}{5}-\dfrac{5}{2}\)
\(=\dfrac{-300+6-25}{10}=\dfrac{-319}{10}\)
h) \(5\sqrt{9}-4\sqrt{\dfrac{1}{16}}+6\sqrt{25}\)
\(=5.3-4.\dfrac{1}{4}+6.5\)
\(=15-1+30\)
\(=14+30\)
\(=44\)
g) \(10\sqrt{\dfrac{9}{25}}-14\sqrt{\dfrac{36}{49}}+24\sqrt{\dfrac{81}{64}}\)
\(=10.\dfrac{3}{5}-14.\dfrac{6}{7}+24.\dfrac{9}{8}\)
\(=6-12+27\)
\(=\left(-6\right)+27=21\)
Câu 3:
a) \(\sqrt{x}=7\)
\(=>x=49\)
b) \(\sqrt{x}=12\)
\(=>x=144\)
c) \(\sqrt{x}=15\)
\(=>x=225\)
d) \(\sqrt{x}=20\)
\(=>x=400\)
e) \(4\sqrt{x}=8\)
\(\sqrt{x}=8:4\)
\(\sqrt{x}=2\)
\(=>x=4\)
f) \(6\sqrt{x}=3\)
\(\sqrt{x}=\dfrac{3}{6}=\dfrac{1}{2}\)
\(=>x=\dfrac{1}{4}\)
g) \(\sqrt{x-1}=1\)
\(x-1=1\)
\(x=1+1\)
\(=>x=2\)
h) \(\sqrt{x+1}=2\)
\(x+1=4\)
\(x=4-1\)
\(=>x=3\)
i) \(\sqrt{x}-2=7\)
\(\sqrt{x}=7+2\)
\(\sqrt{x}=9\)
\(=>x=81\)
j) \(14-\sqrt{x}=12\)
\(\sqrt{x}=14-12\)
\(\sqrt{x}=2\)
\(=>x=4\)
k) \(12-\sqrt{x-1}=2\)
\(\sqrt{x-1}=12-2\)
\(\sqrt{x-1}=10\)
\(x-1=100\)
\(x=100+1\)
\(=>x=101\)
l) \(\sqrt{x+5}+10=20\)
\(\sqrt{x+5}=20-10\)
\(\sqrt{x+5}=10\)
\(x+5=100\)
\(x=100-5\)
\(=>x=95\)
# Wendy Dang
3:
a: ĐKXĐ: x>=0
\(\sqrt{x}=7\)
=>x=7^2=49
b: ĐKXĐ: x>=0
\(\sqrt{x}=12\)
=>x=12^2=144
c: ĐKXĐ: x>=0
\(\sqrt{x}=15\)
=>x=15^2=225
d: ĐKXĐ: x>=0
\(\sqrt{x}=20\)
=>x=20^2=400
e: ĐKXĐ: x>=0
\(4\sqrt{x}=8\)
=>\(\sqrt{x}=2\)
=>x=4
f: ĐKXĐ: x>=0
\(6\cdot\sqrt{x}=3\)
=>\(\sqrt{x}=\dfrac{3}{6}=\dfrac{1}{2}\)
=>x=1/4
g: ĐKXĐ: x>=1
\(\sqrt{x-1}=1\)
=>x-1=1
=>x=2
h: ĐKXĐ: x>=-1
\(\sqrt{x+1}=2\)
=>x+1=4
=>x=3
i: ĐKXĐ: x>=0
\(\sqrt{x}-2=7\)
=>\(\sqrt{x}=9\)
=>x=81
j: ĐKXĐ: x>=0
\(14-\sqrt{x}=12\)
=>\(\sqrt{x}=14-12=2\)
=>x=4
k: ĐKXĐ: x>=1
\(12-\sqrt{x-1}=2\)
=>\(\sqrt{x-1}=10\)
=>x-1=100
=>x=101
i: ĐKXĐ: x>=-5
\(\sqrt{x+5}+10=20\)
=>\(\sqrt{x+5}=10\)
=>x+5=100
=>x=95

\(\frac{-3}{7}\).\(^{\left(-3\right)^2}\)-\(\sqrt{\frac{4}{49}}\)
= \(\frac{-3}{7}.9-\sqrt{\frac{4}{49}}\)
=\(\frac{-27}{7}-\sqrt{\frac{4}{49}}\)
=\(\frac{-27}{7}-\frac{2}{7}\)
=\(\frac{-29}{7}\)
Chúc bạn học tốt
\(\left|-\frac{3}{7}\right|\cdot(-3)^2-\sqrt{\frac{4}{49}}\)
\(=\frac{3}{7}\cdot9-\frac{2}{7}\)
\(=\frac{27}{7}-\frac{2}{7}=\frac{25}{7}\)



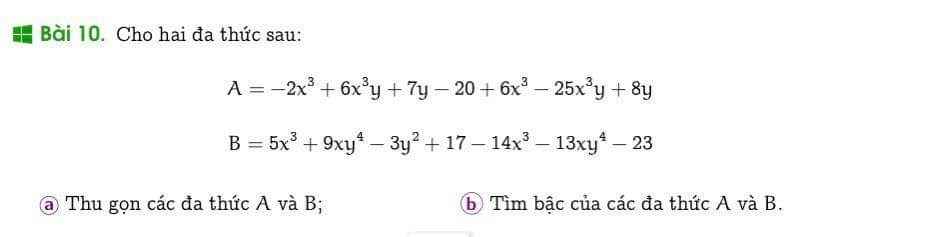 Giúp mik vớii ( chi tiết nếu đc ạ)
Giúp mik vớii ( chi tiết nếu đc ạ) 
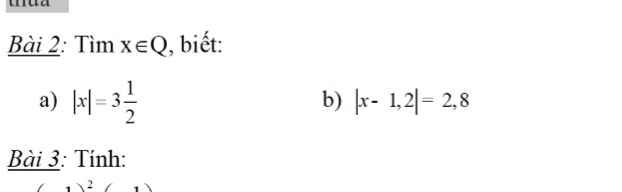




b: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
\(=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}\)
\(=k^2\)(1)
Ta có: \(\dfrac{a^2-c^2}{b^2-d^2}\)
\(=\dfrac{\left(bk\right)^2-\left(dk\right)^2}{b^2-d^2}\)
\(=k^2\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{a^2-c^2}{b^2-d^2}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{4a+3c}{4b+3d}=\dfrac{4bk+3dk}{4b+3d}=k\)
\(\dfrac{4a-3c}{4b-3d}=\dfrac{4bk-3dk}{4b-3d}=k\)
Do đó: \(\dfrac{4a+3c}{4b+3d}=\dfrac{4a-3c}{4b-3d}\)