
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40

Bài 2:
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
d: \(AH^2-AN^2=HN^2\)
\(BH^2-BM^2=MH^2\)
mà HN=MH
nên \(AH^2-AN^2=BH^2-BM^2\)
hay \(AH^2+BM^2=BH^2+AN^2\)

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
Suy ra: BA=BH
b: Ta có: ΔBAD=ΔBHD
nên DA=DH
mà DH<DC
nên DA<DC
a, Xét tam giác ABD và tam giác HBD
^ABH = ^HBD (gt)
BD _ chung
Vậy tam giác ABD = tam giác HBD (ch-gn)
=> BA = BH ( 2 cạnh tương ứng )
b, Lại có AD = DH ( 2 cạnh tương ứng )
Xét tam giác DHC vuông tại H
có DC > DH ( cạnh huyền > cạnh góc vuông )
=> AD < DC

\(\dfrac{x-1}{3}=\dfrac{2-x}{-2}\)
⇔ \(\dfrac{x-1}{3}=\dfrac{x-2}{2}\)
⇔ \(3x-6-2x+2=0\)
⇔ \(x-4=0\)
⇒ \(x=4\)

Câu 4:
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra:HD=HE

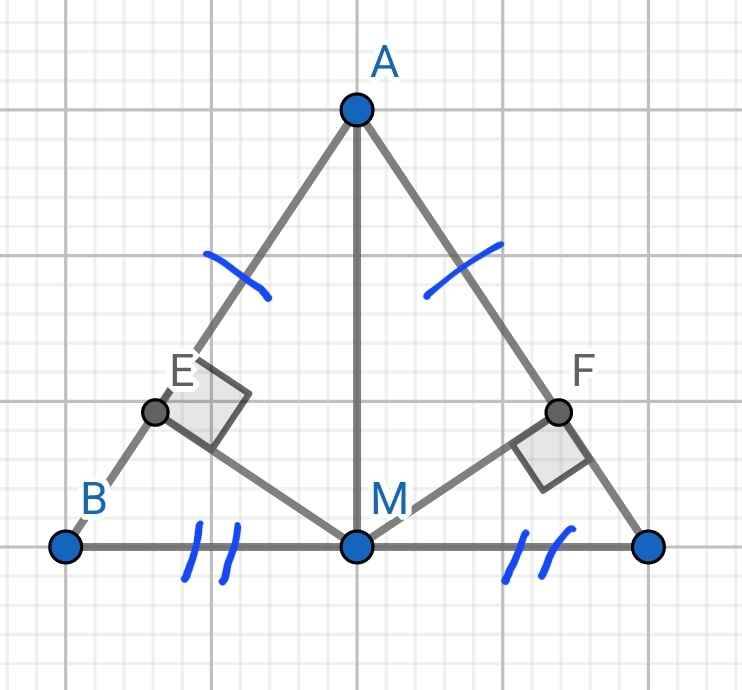
a) Xét ∆ABM và ∆ACM có:
AB = AC (∆ABC cân tại A)
BM = CM (AM là trung tuyến)
AM chung
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ ∠BAM = ∠CAM (hai góc tương ứng)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AEM và ∆AFM có:
AM chung
∠EAM = ∠FAM (cmt)
⇒ ∆AEM = ∆AFM (cạnh huyền - góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)

a: Xét ΔDOE vuông tại O và ΔKOE vuông tại O có
EO chung
\(\widehat{DEO}=\widehat{KEO}\)
Do đó: ΔDOE=ΔKOE
b: Xét ΔEDI vàΔEKI có
ED=EK
\(\widehat{DEI}=\widehat{KEI}\)
EI chung
Do đó: ΔEDI=ΔEKI
Suy ra: \(\widehat{EDI}=\widehat{EKI}=90^0\)
hay IK\(\perp\)FE
c: Xét ΔDIQ vuông tại D và ΔKIF vuông tại K có
ID=IK
\(\widehat{DIQ}=\widehat{KIF}\)
Do đó: ΔDIQ=ΔKIF
Suy ra: IQ=IF


1:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
mà góc BAC=90 độ
nên ABDC là hình chữ nhật
=>AB//CD và AB=CD
b: Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
=>ΔABC=ΔCDA
c: ΔCBA vuông tại A
mà AM là trung tuyến
nên AM=BC/2
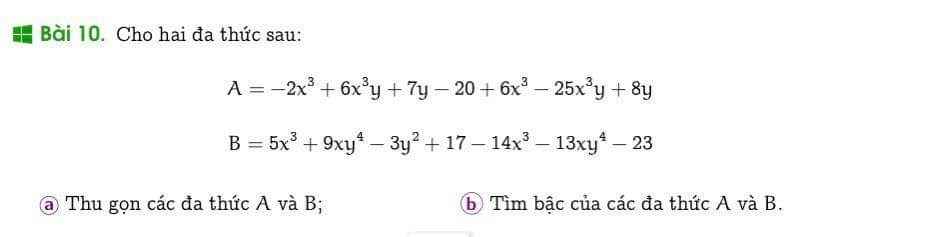 Giúp mik vớii ( chi tiết nếu đc ạ)
Giúp mik vớii ( chi tiết nếu đc ạ) 

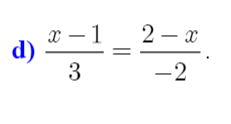




Lời giải:
a.
$A=(-2x^3+6x^3)+(6x^3y-25x^3y)+(7y+8y)-20$
$=4x^3-19x^3y+15y-20$
b.
$B=(5x^3-14x^3)+(9xy^4-13xy^4)-3y^2+(17-23)$
$=-9x^3-4xy^4-3y^2-6$
b.
Bậc của $A$ gắn với $-19x^3y$, là $3+1=4$
Bậc của $B$ gắn với $-4xy^4$, là $1+4=5$
ab, \(A=-2x^3-19x^3y+15y-20\)
-> bậc 4
\(B=-9x^3-4xy^4-3y^2-5\)
-> bậc 5