Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 3:
a) Thay x=9 vào A, ta được:
\(A=\dfrac{3+2}{3-5}=\dfrac{5}{-2}=\dfrac{-5}{2}\)
b) Ta có: M=B:A
\(=\left(\dfrac{x+3\sqrt{x}}{x-25}+\dfrac{1}{\sqrt{x}-5}\right):\dfrac{\sqrt{x}+2}{\sqrt{x}-5}\)
\(=\dfrac{x+3\sqrt{x}+\sqrt{x}+5}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+2}\)
\(=\dfrac{x+4\sqrt{x}+5}{x+7\sqrt{x}+10}\)

Bài 4:
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
hay O,B,A,C cùng thuộc 1 đường tròn
Bài 5:
\(\sqrt{x+2021}-y^3=\sqrt{y+2021}-x^3\\ \Leftrightarrow\left(\sqrt{x+2021}-\sqrt{y+2021}\right)+\left(x^3-y^3\right)=0\\ \Leftrightarrow\dfrac{x-y}{\sqrt{x+2021}+\sqrt{y+2021}}+\left(x-y\right)\left(x^2+xy+y^2\right)=0\\ \Leftrightarrow\left(x-y\right)\left(\dfrac{1}{\sqrt{x+2021}+\sqrt{y+2021}}+x^2+xy+y^2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-y=0\\\dfrac{1}{\sqrt{x+2021}+\sqrt{y+2021}}+x^2+xy+y^2=0\left(1\right)\end{matrix}\right.\)
Dễ thấy \(\left(1\right)>0\) với mọi x,y
Do đó \(x-y=0\) hay \(x=y\)
\(\Leftrightarrow M=x^2+2x^2-2x^2+2x+2022=x^2+2x+1+2021\\ \Leftrightarrow M=\left(x+1\right)^2+2021\ge2021\)
Dấu \("="\Leftrightarrow x=y=-1\)

c: Xét ΔBAC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\left(1\right)\)
Xét ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=BK\cdot BM\)

Câu 15:
Gọi $x_0$ là nghiệm chung của 2 pt thì:
\(\left\{\begin{matrix}
x_0^2+ax_0+1=0\\
x_0^2-x_0-a=0\end{matrix}\right.\Rightarrow x_0(a+1)+(a+1)=0\)
\(\Leftrightarrow (x_0+1)(a+1)=0\)
Hiển nhiên $a\neq -1$ để 2 PT không trùng nhau. Do đó $x_0=-1$ là nghiệm chung của 2 PT
Thay vào:
$(-1)^2+a(-1)+1=0$
$\Leftrightarrow 1-a+1=0\Rightarrow a=2$
Đáp án C.
Câu 16:
D sai. Trong tam giác vuông tại $A$ là $ABC$, $\cos (90^0-\widehat{B})=\cos \widehat{C}$ và không có cơ sở để khẳng định $\cos \widehat{C}=\sin \widehat{C}$


Lời giải:
Đặt \(\sqrt[3]{5\sqrt{2}+7}=m; \sqrt[3]{5\sqrt{2}-7}=n\)
\(m^3-n^3=14\)
\(mn=1\)
\((a+b+c)^3=(m-n)^3=m^3-3mn(m-n)-n^3=14-3(m-n)\)
\(\Leftrightarrow (a+b+c)^3=14-3(a+b+c)\)
\(\Leftrightarrow (a+b+c)^3+3(a+b+c)-14=0\)
\(\Leftrightarrow (a+b+c)^2[(a+b+c)-2]+2(a+b+c)(a+b+c-2)+7(a+b+c-2)=0\)
\(\Leftrightarrow (a+b+c-2)[(a+b+c)^2+2(a+b+c)+7]=0\)
Dễ thấy biểu thức trong ngoặc vuông $>0$ nên $a+b+c-2=0$
$\Leftrightarrow a+b+c=2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-1}{2}=\frac{3}{2}$

Bài 18:
a: Ta có: \(P=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2\cdot\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)^2\cdot\left(\sqrt{a}+1\right)^2}{4a}\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{\left(a-1\right)\cdot\left(-4\right)\cdot\sqrt{a}}{4a}\)
\(=\dfrac{-a+1}{\sqrt{a}}\)
b: Để P<0 thì -a+1<0
\(\Leftrightarrow-a< -1\)
hay a>1
c: Để P=-2 thì \(-a+1=-2\sqrt{a}\)
\(\Leftrightarrow-a+1+2\sqrt{a}=0\)
\(\Leftrightarrow a-2\sqrt{a}+1=2\)
\(\Leftrightarrow\left(\sqrt{a}-1\right)^2=2\)
\(\Leftrightarrow\sqrt{a}-1=\sqrt{2}\)
hay \(a=3+2\sqrt{2}\)
Bài 17:
a: Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}-1}{\sqrt{a}+1}\right)\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{a-1}\)
\(=2+\dfrac{2a+2}{\sqrt{a}}\)
\(=\dfrac{2a+2\sqrt{a}+2}{\sqrt{a}}\)







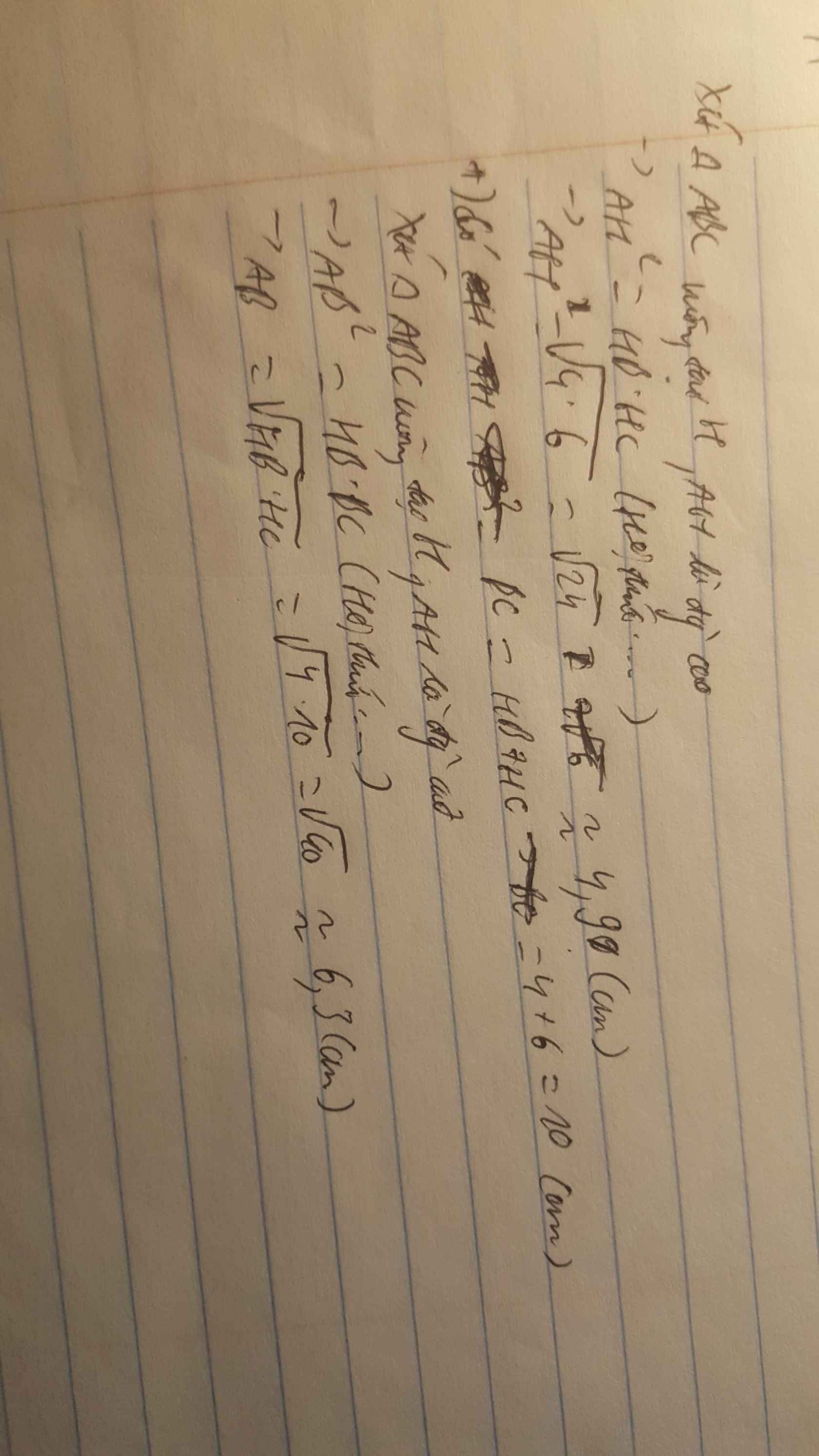

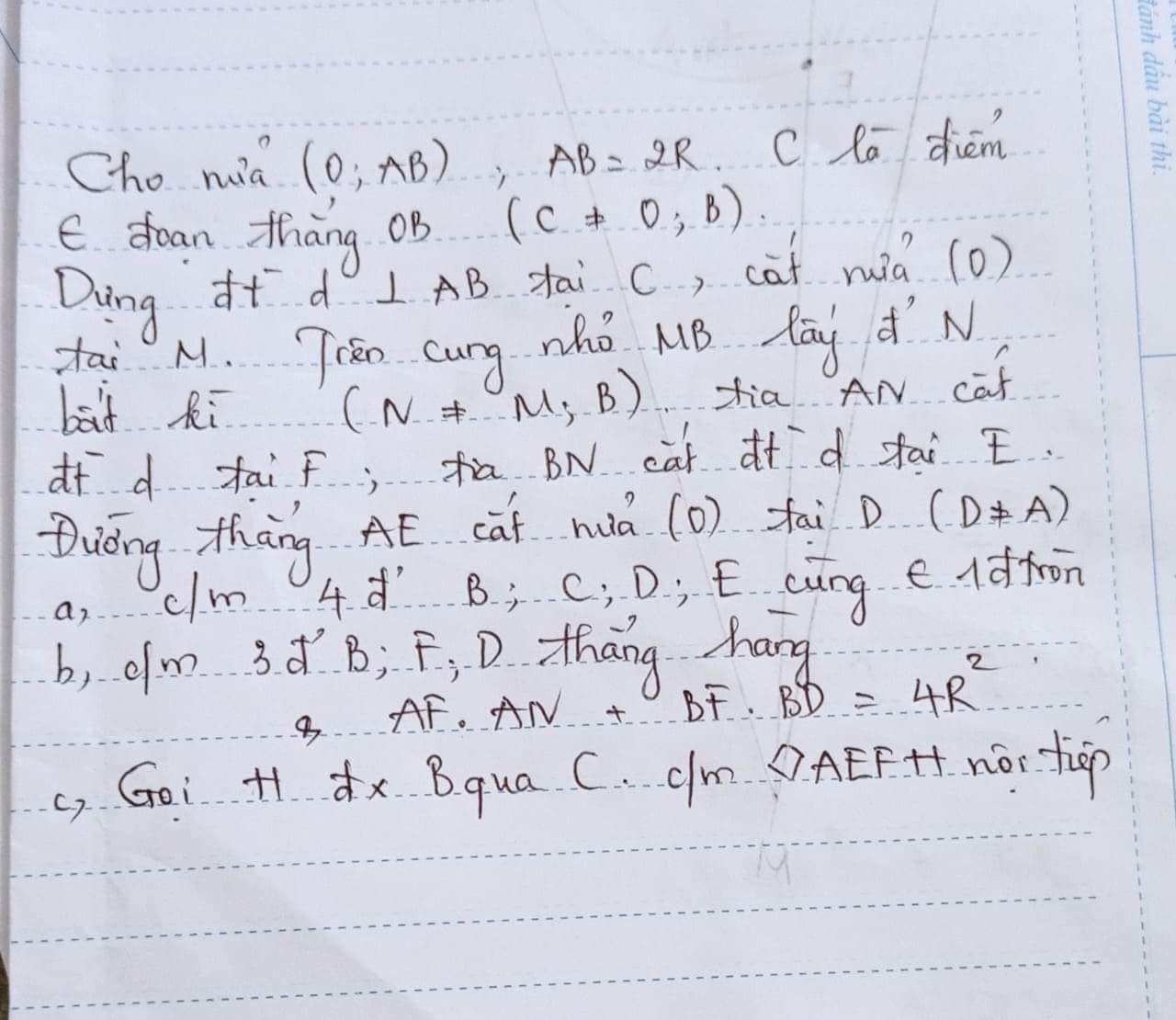

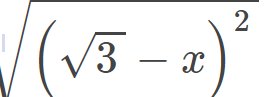
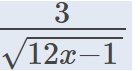 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ