
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


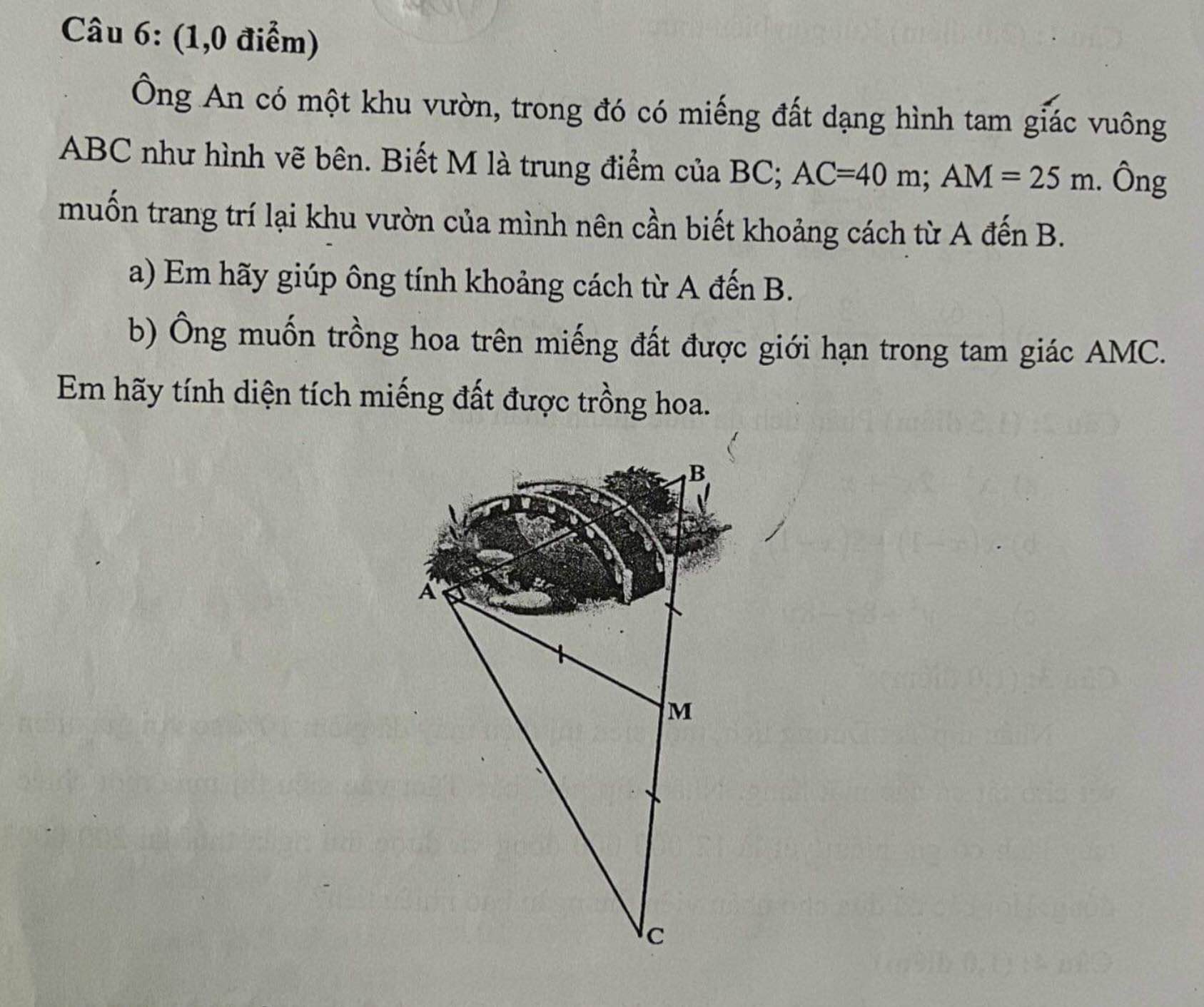
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)



a: Ta có: \(8x\left(x-2017\right)-2x+4034=0\)
\(\Leftrightarrow\left(x-2017\right)\left(4x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\)
c: Ta có: \(4-x=2\left(x-4\right)^2\)
\(\Leftrightarrow2\left(x-4\right)^2+x-4=0\)
\(\Leftrightarrow\left(x-4\right)\left(2x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{7}{2}\end{matrix}\right.\)

3: Ta có: \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-1\right)\left(x+1\right)=27\)
\(\Leftrightarrow x^3-27-x^3+x=27\)
hay x=54

XXét tứ giác AMDN có ^AMD=^MAN=^AND=90∞
⇒AMDN là hình chữ nhật
hcn AMDN có AD là phân giác góc A
⇒AMDN là hình vuông(dấu hiệu 3)

\(a,A=\left(2x-7\right)^2=\left(2\cdot4-7\right)^2=1\\ B=\left(x-3\right)^3=\left(5-3\right)^3=8\\ C=\left(x^2-6x+9+x^2+6x+9\right):\left(x^2+9\right)\\ C=\left(2x^2+18\right):\left(x^2+9\right)=2\left(x^2+9\right):\left(x^2+9\right)\\ C=2\\ D=\left(5x-11-5x+9\right)^2=\left(-2\right)^2=4\)
a) \(A=4x^2-28x+49=\left(2x-7\right)^2=\left(2.4-7\right)^2=1^2=1\)
b) \(B=x^3-9x^2+27x-27=\left(x-3\right)^3\)
\(=\left(5-3\right)^3=2^3=8\)
c) \(C=\left[\left(x-3\right)^2+\left(x+3\right)^2\right]:\left(x^2+9\right)=\left(x^2-6x+9+x^2+6x+9\right):\left(x^2+9\right)=\left[2\left(x^2+9\right)\right]:\left(x^2+9\right)=2\)
d) \(D=\left(5x-11\right)^2-2\left(5x-11\right)\left(5x-9\right)+\left(5x-9\right)^2=\left(5x-11-5x+9\right)^2=\left(-2\right)^2=4\)

a: \(4x^2-6x=2x\left(2x-3\right)\)
b: \(9x^4y^3+3x^2y^4=3x^2y^3\left(3x^2+y\right)\)
c: \(x^3-2x^2+5x=x\left(x^2-2x+5\right)\)
d: \(3x\left(x-1\right)+5\left(x-1\right)=\left(x-1\right)\left(3x+5\right)\)
e: \(2x^2\left(x+1\right)+4\left(x+1\right)=2\left(x+1\right)\left(x^2+2\right)\)
f: \(-3x-6xy+9xz=-3x\left(1+2y-3z\right)\)


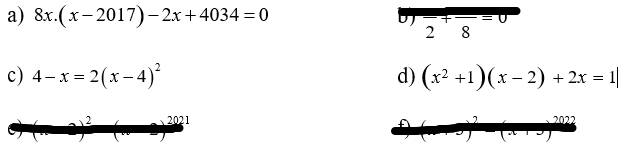
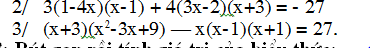

 giúp mình với plzzz , chiều mình nộp r ạ
giúp mình với plzzz , chiều mình nộp r ạ 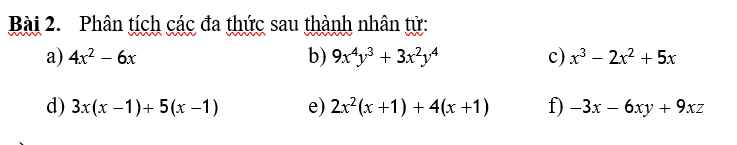
A. Trắc nghiệm: 1.A; 2.B; 3.D; 4.D; 5.B; 6.C; 7.B; 8.C
B. Tự luận
Bài 4:
a/ Ta có AB//CD; \(AM\in AB;CN\in CD\) => AM//CN
AN//CM (gt)
=> AMCN là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi 1 là hbh)
b/ Ta có
AD//CD; \(CI\in BC\) => AD//CI
AD=BC mà BC=CI => AD=CI
=> ACID là hbh (Tứ giác có cặp cạnh đối // và bằng nhau là hbh) => AC=DI (trong hbh các cặp cạnh đối = nhau từng đôi 1)
c/
Ta có
AM=BM (gt) \(\Rightarrow AM=\frac{AB}{2}\) mà AB=CD \(\Rightarrow AM=\frac{CD}{2}\)
Mà AMCN là hbh => AM=CN => \(CN=\frac{CD}{2}\) => N là trung điểm của CD (1)
AMCN là hbh => OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => O là trung điểm của AC (2)
Từ (1) và (2) => NO là đường trung binhd của tg ACD (đường thẳng đi qua trung điểm của 2 cạnh một tam giác là đường trung bình)
d/ Trong hbh ACID nối AI cắt CD tại N' => N' là trung điểm của CD (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Mà N là trung điểm của CD (cmt)
=> N trùng N'
Ta có
AMCN là hbh => MC//AN (Trong hbh các cặp cạnh đối // với nhau từng đôi 1)
Mà \(NI\in AN\)
=> MC//NI
Bài 5
\(A=-\left(y^4-8y^2+16\right)+20=-\left(y^2-4\right)^2+20\)
Ta có \(\left(y^2-4\right)\ge0\Rightarrow-\left(y^2-4\right)^2\le0\)
\(\Rightarrow A=-\left(y^2-4\right)+20\le20\)
Vậy giá trị lớn nhất của A là 20
Bài 5 (tiếp)
\(-\left(y^2-4\right)+20=20\Rightarrow y^2-4=0\Rightarrow y^2=4\Rightarrow y=\pm2\)