
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật


b:
Ta có: MN\(\perp\)AC
AB\(\perp\)AC
Do đó: MN//AB
Xét ΔACB có
M là trung điểm của BC
MN//AB
Do đó: N là trung điểm của AC
=>\(\dfrac{AN}{AC}=\dfrac{1}{2}\)
c:
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
=>MA=MB
=>ΔMAB cân tại M
Ta có: \(\widehat{DAB}+\widehat{MAB}=\widehat{MAD}=90^0\)
\(\widehat{HAB}+\widehat{HBA}=90^0\)(ΔHAB vuông tại H)
mà \(\widehat{MAB}=\widehat{HBA}\)(ΔMAB cân tại M)
nên \(\widehat{DAB}=\widehat{HAB}\)
=>AB là tia phân giác của góc DAH

Giải:
Gọi x là năng suất dự tính của xí nghiệp (sản phẩm/ngày); (x ∈ N*) .
⇒ Số thảm len dệt được theo dự tính là: 20x (thảm).
Sau khi cải tiến, năng suất của xí nghiệp đã tăng 20% nên năng suất trên thực tế là:
x + 20%.x = x + 0,2x = 1,2x (sản phẩm/ngày)
Sau 18 ngày, xí nghiệp dệt được:
18.1,2x = 21,6.x (thảm).
Vì sau 18 ngày, xí nghiệp không những hoàn thành số thảm cần dệt mà còn dệt thêm được 24 tấm nên ta có phương trình:
21,6.x = 20x + 24
⇔ 21,6x – 20x = 24
⇔ 1,6x = 24
⇔ x = 15 (thỏa mãn)
Vậy số thảm mà xí nghiệp phải dệt ban đầu là: 20.15 = 300 (thảm).

a: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BH//CDvà BD//CH
BH//CD
AC vuông góc BH
Do đó: CA vuông góc CD
=>ΔCAD vuông tại C
CH//BD
CH vuông góc AB
Do đó: BD vuông góc AB
=>ΔABD vuông tại B
c: \(\widehat{ABD}=\widehat{ACD}=90^0\)
=>ABDC là tứ giác nội tiếp đường tròn đường kính AD
=>ABDC nội tiếp (I)
=>IA=IB=ID=IC

3.(⅓x - ¼)² = ⅓
=> (\(\dfrac{1}{3x}\)- \(\dfrac{1}{4}\) )2 = \(\dfrac{1}{9}\)
=>\(\left[{}\begin{matrix}\dfrac{1}{3x}-\dfrac{1}{4}=\dfrac{-1}{3}\\\dfrac{1}{3x}-\dfrac{1}{4}=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\dfrac{1}{3x}=\dfrac{-1}{12}\\\dfrac{1}{3x}=\dfrac{7}{12}\end{matrix}\right.\) => \(\left[{}\begin{matrix}x=-4\\x=\dfrac{12}{21}=\dfrac{4}{7}\end{matrix}\right.\)
Vậy, tập nghiệm x thỏa mãn là S=\(\left\{-4;\dfrac{4}{7}\right\}\)

Dễ thấy x=0 không phải là nghiệm của phương trình.
Khi đó phương trình tương đương:
\(x^2+x+2+\dfrac{1}{x}+\dfrac{1}{x^2}=0\)
\(\Leftrightarrow\left(x^2+\dfrac{1}{x^2}+2\right)+\left(x+\dfrac{1}{x}\right)=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+\left(x+\dfrac{1}{x}\right)=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)\left(x+\dfrac{1}{x}+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{x}=0\\x+\dfrac{1}{x}+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\\x^2+x+1=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình vô nghiệm.

/x-1/+x-2/=1 (1)
Bảng xét dấu:
| x | 1 | 2 | ||
| x-1 | -0 | + | bạn kéo 1 gạch đứng | + |
| x-2 | - bạn kéo 1 gạch đứng nha! | - | 0 | + |
TH1: x<1 thì (1) <=> 1-x+2-x=1
-2x + 3 = 1
- 2x = -1
x = 1 (KTM)
TH2:với 1< hoặc = x bé hơn hoặc = 2 thì ta có:
(1) <=> x-1+2-x=1
0x + 1 = 1
0x = 0 ( vô lý ) => (KTM)
TH3: với x>2 thì ta có:
(1) <=> x-1+x-2=1
2x -3 = 1
2x = 4
x = 2
vậy k có giá trị nào thỏa mãn
\(\Leftrightarrow|^{ }_{ }x-1|^{ }_{ }+|^{ }_{ }2-x|^{ }_{ }=1\)
co \(|^{ }_{ }x-1|^{ }_{ }\ge x-1\)voi moi x
\(|^{ }_{ }2-x|^{ }_{ }\ge2-x\)voi moi x
\(\Rightarrow|^{ }_{ }x-1|^{ }_{ }+|^{ }_{ }2-x|^{ }_{ }\ge x-1+2-x=1\)
dau bang xay ra \(\Leftrightarrow\hept{\begin{cases}x-1\ge0\\2-x\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge1\\x\le2\end{cases}}\Leftrightarrow1\le x\le2\)
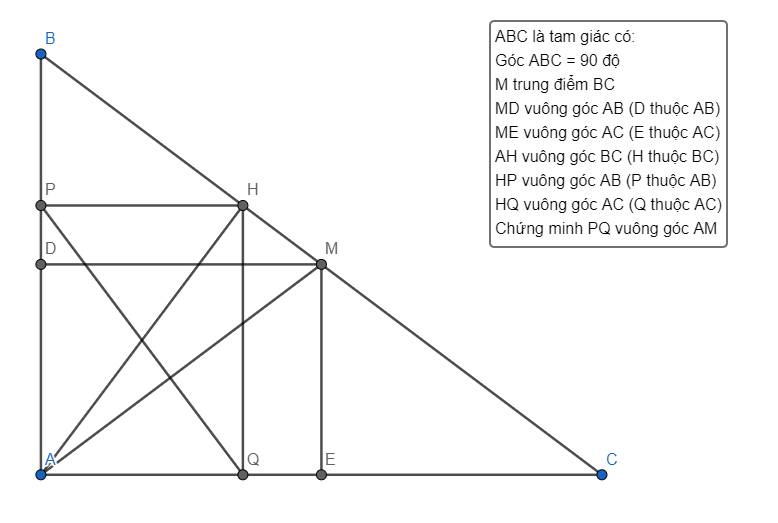




 Vẽ hình và giải chi tiết giúp mình nhé. Mình đang cần gấp.
Vẽ hình và giải chi tiết giúp mình nhé. Mình đang cần gấp.
Xét tg vuông ABC
\(MB=MC\left(gt\right)\Rightarrow MA=MB=MC=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Xét tg MAC có
MA=MC (cmt) => tg MAC cân tạo M \(\Rightarrow\widehat{MAC}=\widehat{ACB}\) (1)
\(\widehat{ABC}=\widehat{HAC}\) (cùng phụ với \(\widehat{ACB}\) ) (2)
Gọi O là giao của AH và PQ
Xét tứ giác APHQ có
\(AB\perp AC\left(gt\right);HQ\perp AC\left(gt\right)\) => AB//HQ
\(AC\perp AB\left(gt\right);HP\perp AB\left(gt\right)\) => AC//HP
=> APHQ là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi 1 là hbh)
Mà \(\widehat{A}=90^o\left(gt\right)\) => APHQ là hình chữ nhật
\(\Rightarrow AH=PQ\) (2 đường chéo HCN băng nhau)
Mà OA=OH; OP= OQ (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> OA=OH=OP=OQ => tg OAQ là tg cân tạo O
\(\Rightarrow\widehat{HAC}=\widehat{AQP}\) (góc ở đáy tg cân) (3)
Từ (2) và (3) \(\Rightarrow\widehat{ABC}=\widehat{AQP}\) (4)
Xét tg vuông ABC có \(\widehat{ABC}+\widehat{ACB}=90^o\) (5)
Từ (1) (4) (5) \(\Rightarrow\widehat{AQP}+\widehat{MAC}=90^o\)
Gọi K là giao của PQ và AM, xét tg AKQ có
\(\widehat{AKQ}=180^o-\left(\widehat{AQP}+\widehat{MAC}\right)=180^o-90^o=90^o\)
\(\Rightarrow PQ\perp AM\left(dpcm\right)\)