
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x.y=\frac{x}{y}\)
\(\Rightarrow y^2=\frac{x}{x}=1\)
\(\Rightarrow y=1;-1\)
Nếu \(y=1\Rightarrow x+1=x\)( điều này ko thể xảy ra )
Nếu \(y=-1\Rightarrow x-1=-x\Rightarrow x=\frac{1}{2}\)
Vậy \(x=\frac{1}{2};y=-1\)

Một tỉ lệ thức \(\frac{a}{b}=\frac{c}{d}\) có các số hang khác nhau, nếu \(a\ne b,a\ne c,a\ne d,b\ne c,b\ne d,c\ne d\) và \(a.d=b.c\)
Xét các nhóm 4 phần tử của A có tích hai số này bằng tích hai số kia, ta có:
Với \(\left\{4,8,16.32\right\}\) thì \(4.32=8.16\) và có các tỉ lệ thức:
\(\frac{16}{32}=\frac{4}{8};\frac{8}{32}=\frac{4}{16};\frac{32}{16}=\frac{8}{4};\frac{32}{8}=\frac{16}{4}\)
Với \(\left\{4,8,32,64\right\}\) thì \(4.64=8.32\) và có các tỉ lệ thức:
\(\frac{4}{8}=\frac{32}{64};\frac{4}{32}=\frac{8}{64};\frac{8}{4}=\frac{64}{32};\frac{32}{4}=\frac{64}{8}\)
Với \(\left\{8,16,32,64\right\}\) thì \(8.64=16.32\) và có các tỉ lệ thứ:
\(\frac{8}{32}=\frac{16}{64};\frac{8}{16}=\frac{32}{64};\frac{32}{8}=\frac{64}{16};\frac{16}{8}=\frac{64}{32}\)

a) Xét tam giác ABD và tam giác EBD có:
AB = EB (gt).
^ABD = ^EBD (BD là phân giác).
BD chung.
=> Tam giác ABD = tam giác EBD (c - g - c).
=> DA = DE (cặp cạnh tương ứng).
b) Tam giác ABD = tam giác EBD (cmt).
=> ^BAD = ^BED (cặp góc tương ứng).
Mà ^BAD = 90 độ (tam giác ABC vuông tại A).
=> ^BED = 90 độ.
c) Xét tam giác KBC có:
CA là đường cao (^CAB = 90 độ).
KE là đường cao (^KEC = 90 độ).
Mà D là giao điểm của CA và KE.
=> D là trực tâm của tam giác KBC.
=> BD là đường cao.
=> BD vuông góc KC. (1)
Xét tam giác KBC có:
BD là đường cao (cmt).
BD là phân giác góc KBC (gt).
=> Tam giác KBC cân tại B.
Xét tam giác ABE có:
BE = BA (gt).
=> Tam giác ABE cân tại B.
Xét tam giác ABE cân tại B có:
BD là phân giác góc ABE (gt).
=> BD là đường cao (tính chất các đường trong tam giác cân).
=> BD vuông góc AE. (2)
Từ (1); (2) => AE // KC ( từ vuông góc đến song song).

a) Xét tam giác ABM và tam giác CDM có:
+ BM = DM (M là trung điểm BD).
+ ^AMB = ^CMD (đối đỉnh).
+ AM = CM (M là trung điểm AC).
=> Tam giác ABM = Tam giác CDM (c - g - c).
b) Vì tam giác ABM = tam giác CDM (cmt).
=> AB = CD (2 cạnh tương ứng).
Ta có: ^BAM = 90o (Tam giác ABC vuông tại A).
Mà ^BAM = ^DCM (tam giác ABM = tam giác CDM).
=> ^BAM = ^DCM = 90o.
=> CD vuông góc AC (đpcm).
c) Ta có: AB = CD (cmt).
Mà CD = CE (gt).
Xét tứ giác ACEB có:
+ AB = CE (cmt).
+ AB // AC (do cùng vuông óc với AC).
=> Tứ giác ADEB là hình bình hành (dhnb).
=> Giao điểm của 2 đường chéo BC và AE là trung điểm của mỗi đường (Tính chất hình bình hành).
Mà O là trung điểm của BC (gt).
=> O là trung điểm của AE.
=> 3 điểm A; O; E thẳng hàng (đpcm).




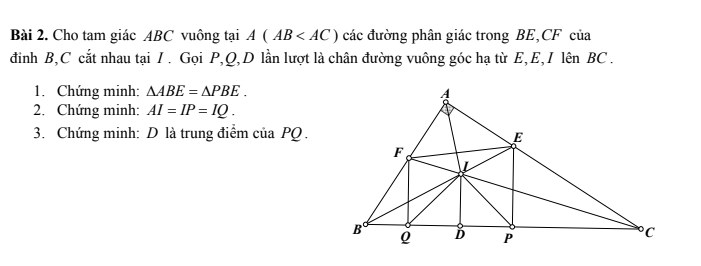
câu 1
câu 2
câu a
ta có K1 = H2=90 độ
mà 2 góc trên ở vị trí so le trong
=>a//b
câu b
K2=70 độ (kề bù)
H1=70 độ (kề bù)
N3=70 độ (đối đỉnh)
I1=70 độ (đồng vị)