K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TK
1
29 tháng 7 2023
1: A=-1/2*xy^3*4x^2y^2=-2x^3y^5
Bậc là 8
Phần biến là x^3;y^5
Hệ số là -2
2:
a: P(x)=3x+4x^4-2x^3+4x^2-x^4-6
=3x^4-2x^3+4x^2+3x-6
Q(x)=2x^4+4x^2-2x^3+x^4+3
=3x^4-2x^3+4x^2+3
b: A(x)=P(x)-Q(x)
=3x^4-2x^3+4x^2+3x-6-3x^4+2x^3-4x^2-3
=3x-9
A(x)=0
=>3x-9=0
=>x=3
15 tháng 7 2021
a) Xét ΔOBH và ΔODA có
OB=OD(gt)
\(\widehat{BOH}=\widehat{DOA}\)(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: \(\widehat{OHB}=\widehat{OAD}\)(hai góc tương ứng)
mà \(\widehat{OHB}=90^0\)(gt)
nên \(\widehat{OAD}=90^0\)
hay AH\(\perp\)AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
\(\widehat{AOE}=\widehat{HOC}\)(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
PT
15 tháng 7 2021
) Xét ΔOBH và ΔODA có
OB=OD(gt)
ˆBOH=ˆDOABOH^=DOA^(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: ˆOHB=ˆOADOHB^=OAD^(hai góc tương ứng)
mà ˆOHB=900OHB^=900(gt)
nên ˆOAD=900OAD^=900
hay AH⊥⊥AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
ˆAOE=ˆHOCAOE^=HOC^(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
L
1
11 tháng 10 2021
\(ĐK:x\ge-3\\ PT\Leftrightarrow\sqrt{x-3}=2\Leftrightarrow x-3=4\Leftrightarrow x=7\left(tm\right)\)
22 tháng 10 2021
ý bạn là \(x-y-z=-33?\)
Ta có \(2x=3y=5z\Rightarrow\dfrac{2x}{30}=\dfrac{3y}{30}=\dfrac{5z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x-y-z}{15-10-6}=\dfrac{-33}{-1}=33\\ \Rightarrow\left\{{}\begin{matrix}x=33\cdot15=495\\y=33\cdot10=330\\z=33\cdot6=198\end{matrix}\right.\)
22 tháng 1
Bài 9:
a: Xét ΔAMD vuông tại M và ΔAMI vuông tại M có
AM chung
MD=MI
Do đó: ΔAMD=ΔAMI
Xét ΔAND vuông tại N và ΔANK vuông tại N có
AN chung
ND=NK
Do đó: ΔAND=ΔANK
b: ta có: ΔAMD=ΔAMI
=>\(\widehat{MAD}=\widehat{MAI}\)
=>\(\widehat{DAB}=\widehat{IAB}\)
mà tia AB nằm giữa hai tia AD,AI
nên AB là phân giác của góc DAI
=>\(\widehat{DAI}=2\cdot\widehat{DAB}\)
Ta có: ΔAND=ΔANK
=>\(\widehat{DAN}=\widehat{KAN}\)
=>\(\widehat{DAC}=\widehat{KAC}\)
mà tia AC nằm giữa hai tia AD,AK
nên AC là phân giác của góc DAK
=>\(\widehat{DAK}=2\cdot\widehat{DAC}\)
Ta có: \(\widehat{DAK}+\widehat{DAI}=\widehat{KAI}\)
=>\(\widehat{KAI}=2\cdot\left(\widehat{DAB}+\widehat{DAC}\right)\)
=>\(\widehat{KAI}=2\cdot\widehat{BAC}=180^0\)
=>K,A,I thẳng hàng
c: Ta có: AD=AI(ΔADM=ΔAIM)
AD=AK(ΔADN=ΔAKN)
Do đó: AI=AK
mà K,A,I thẳng hàng
nên A là trung điểm của KI
d: Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
=>AMDN là hình chữ nhật
Hình chữ nhật AMDN có AD là phân giác của góc MAN
nên AMDN là hình vuông
=>DA là phân giác của góc NDM
=>DA là phân giác của góc KDI
Xét ΔDKI có
DA là đường trung tuyến
DA là đường phân giác
Do đó: ΔDKI cân tại D
Ta có: ΔDKI cân tại D
mà DA là đường trung tuyến
nên DA\(\perp\)KI
18 tháng 10 2021
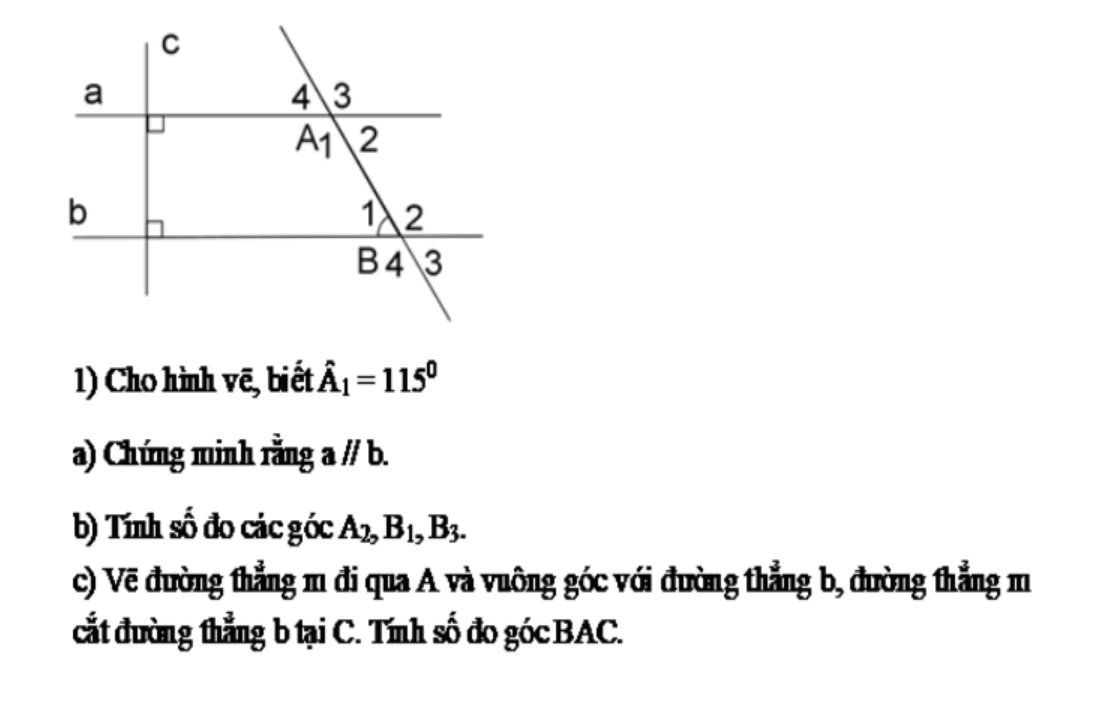
a) Ta có: a⊥c,b⊥c
=> a//b
b) \(\widehat{A_2}+\widehat{A_1}=180^0\)(kề bù)
\(\Rightarrow\widehat{A_2}=180^0-115^0=65^0\)
\(\widehat{B_1}=\widehat{A_2}=65^0\)(so le trong do a//b)
\(\Rightarrow\widehat{B_1}=\widehat{B_3}=65^0\)(đối đỉnh)
TT
2
\(=5+5-3-3=4\)
= 5 + 5 - 3 - 3 = 4