
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: A=-1/2*xy^3*4x^2y^2=-2x^3y^5
Bậc là 8
Phần biến là x^3;y^5
Hệ số là -2
2:
a: P(x)=3x+4x^4-2x^3+4x^2-x^4-6
=3x^4-2x^3+4x^2+3x-6
Q(x)=2x^4+4x^2-2x^3+x^4+3
=3x^4-2x^3+4x^2+3
b: A(x)=P(x)-Q(x)
=3x^4-2x^3+4x^2+3x-6-3x^4+2x^3-4x^2-3
=3x-9
A(x)=0
=>3x-9=0
=>x=3

\(ĐK:x\ge-3\\ PT\Leftrightarrow\sqrt{x-3}=2\Leftrightarrow x-3=4\Leftrightarrow x=7\left(tm\right)\)


Bài 7:
Ta thấy: $\widehat{xOy}+\widehat{yOx'}=\widehat{xOx'}=180^0$
$\widehat{xOy}-\widehat{yOx'}=30^0$
$\Rightarrow \widehat{yOx'}=\frac{180^0-30^0}{2}=75^0$
$\widehat{xOy'}=\widehat{yOx'}=75^0$ (hai góc đối đỉnh)
Bài 8:
$\widehat{AOC}+\widehat{BOD}=140^0$
$\widehat{AOC}=\widehat{BOD}$ (hai góc đối đỉnh)
$\Rightarrow \widehat{AOC}=\widehat{BOD}=\frac{140^0}{2}=70^0$
$\widehat{COB}=180^0-\widehat{AOC}=180^0-70^0=110^0$
$\widehat{DOA}=\widehat{COB}=110^0$ (hai góc đối đỉnh)


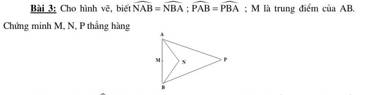
Xét tam giác NAB cân tại N, có M là trung điểm của AB suy ra NM vuông góc với AB (1)
Xét tam giác APB cân tại P, có M là trung điểm của AB suy ra MP vuông góc với AB (2)
Từ (1,2) suy ra M, N, P thẳng hàng
Muốn giải đáp các thắc mắc tới toán , vật lý vui lòng chat trức tiếp

b4: a đúng ; b sai ; c đúng
b5:
(viết B2 ở dưới B1 cho mình nha)
có a⊥b;b⊥c => a // b
Có ∠A1 = ∠B2 (t/c hai đường thẳng song song)
=> ∠B2 = 115o
Mà ∠B1 + ∠B2 = 180o
=> ∠B1 = 180o - ∠B2
= 180o - 115o
=> ∠B1 = 65o

có: tam giác ABO cân tại A (gt)
=> AB=AO (tính chất tam giác cân)
Có: AH vuông góc BO (gt)
=> góc AHB = góc AHO (tính chất đường vuông góc)
Xét tam giác AHB và tam giác AHO có
goc AHB = góc AHO (cmt)
AB = AO (cmt)
AH chung
=> tam giác AHB = tam giác AHO (cạnh huyền - cạnh góc vuông)




S = 22 + 42 + 62 + ... + 202
= (2.1)2 + (2.2)2 + (2.3)2 ... (2.10)2
= 22.12 + 22.22 + 22.32 + ... + 22.102
= 22 (12 + 22 + ... + 102 )
= 4 . 385 = 1540
A=32+62+...+302P=32+62+...+302
=1.32+22.32+...+32.102=1.32+22.32+...+32.102
=32(1+22+...+102)=32(1+22+...+102)
=9.385=3465
Bài này em
\(A=\)\(3^2+6^2+...+30^2\)
\(=\)\(1.3^2+2^2.3^2+...+3^2.10^2\)
\(=\)\(3^2.\left(1+2^2+...+10^2\right)\)
\(=\)\(9.385\)
\(=\)\(3465\)
Vậy \(A=3465\)