AH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TQ
5
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
17 tháng 7 2021
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
14 tháng 12 2021
\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
14 tháng 12 2021
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...
6 tháng 11 2021
\(\sqrt{2x+5}\) xác định khi \(2x+5\ge0\Rightarrow2x\ge-5\Rightarrow x\ge-\dfrac{5}{2}\)
6 tháng 11 2021
\(\sqrt{2x+5}\le0\Leftrightarrow2x+5\le0\Leftrightarrow2x\le-5\Leftrightarrow x\ge\dfrac{-5}{2}\)
\(\Rightarrow\) Đáp án: A
MB
2
6 tháng 11 2021
ĐKXĐ: \(2x-3\ge0\\ \Rightarrow2x\ge0+3\\ \Rightarrow2x\ge3\\ \Rightarrow x\ge\dfrac{3}{2}\left(A\right)\)
MB
4
6 tháng 11 2021
\(\sqrt{3-2x}\) xác định khi \(3-2x\ge0\Rightarrow2x\le3-0\Rightarrow2x\le3\Rightarrow x\le\dfrac{3}{2}\left(D\right)\)
2 tháng 12 2021
\(1,\left\{{}\begin{matrix}3x-y=5\\5x+2y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+2\left(3x-5\right)=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+6x-10=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\11x=33\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3.3-5\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
\(2,\left\{{}\begin{matrix}5x-4y=3\\2x+y=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-4\left(4-2x\right)=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-16+8x=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}13x=19\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=4-2.\dfrac{19}{13}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=\dfrac{14}{13}\end{matrix}\right.\)
NL
1
17 tháng 10 2021
\(4,\\ b,B=\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\ge3\sqrt[3]{\dfrac{xyz}{xyz}}=3\)
Dấu \("="\Leftrightarrow x=y=z\)
\(c,x+y=4\Leftrightarrow x=4-y\\ \Leftrightarrow C=\left(4-y\right)^2+y^2\\ C=16-8y+y^2+y^2=2\left(y^2-4y+4\right)+8\\ C=2\left(y-2\right)^2+8\ge8\\ C_{min}=8\Leftrightarrow x=y=2\)
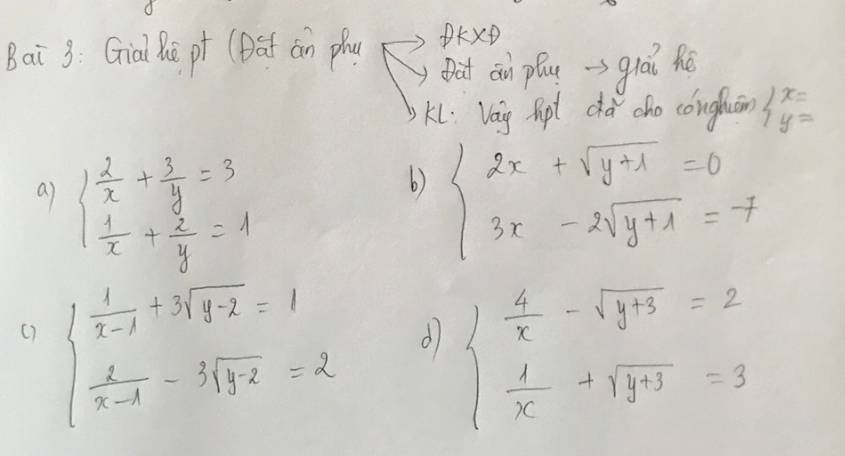
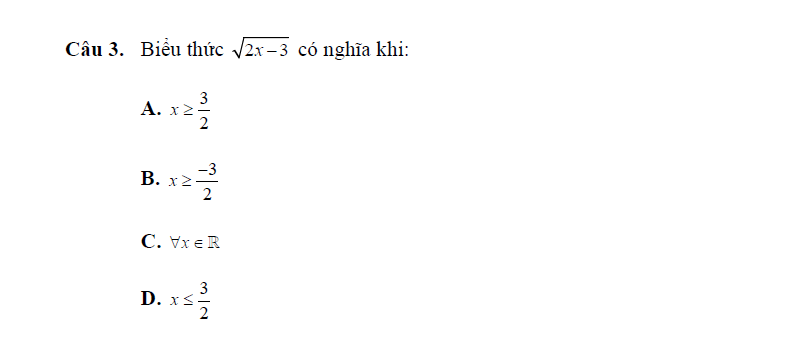
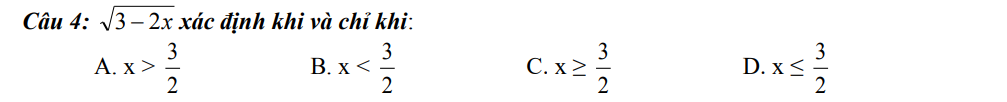
b: ĐKXĐ: y>=-1
Đặt \(\left\{{}\begin{matrix}x=a\\\sqrt{y+1}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
2a+b=0 và 3a-2b=-7
=>4a+2b=0 và 3a-2b=-7
=>a=-1 và b=2
=>x=-1 và y+1=4
=>x=-1 và y=3
c: ĐKXĐ: x<>1 và y>=2
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}=a\\\sqrt{y-2}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
a+3b=1 và 2a-3b=2
=>3a=3 và a+3b=1
=>a=1 và b=0
=>x-1=1 và y-2=0
=>x=2 và y=2
d: ĐKXĐ: x<>0 và y>=-3
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=a\\\sqrt{y+3}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
4a-b=2 và a+b=3
=>5a=5 và a+b=3
=>a=1 và b=2
=>x=1 và y+3=4
=>x=1 và y=1