K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2021
30.
\(V_{\left(O;\dfrac{3}{4}\right)}\left(M\right)=M_1\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{3}{4}.4=3\\y_1=\dfrac{3}{4}.1=\dfrac{3}{4}\end{matrix}\right.\)
\(Q_{\left(O;-90^0\right)}\left(M_1\right)=M'\Rightarrow\left\{{}\begin{matrix}x'=y_1=\dfrac{3}{4}\\y'=-x_1=-3\end{matrix}\right.\)
\(\Rightarrow M'\left(\dfrac{3}{4};-3\right)\)
31.
\(cos\dfrac{x}{2}=-\dfrac{\sqrt{3}}{2}\Rightarrow\dfrac{x}{2}=\pm\dfrac{5\pi}{6}+k2\pi\)
\(\Rightarrow x=\pm\dfrac{5\pi}{3}+k4\pi\)
Nghiệm dương nhỏ nhất \(x=\dfrac{5\pi}{3}\Rightarrow a+b=5+3=8\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
31.
\(y'=4x^3+1\)
Tiếp tuyến vuông góc với \(d\) nên có hệ số góc \(k=5\)
Gọi hoành độ tiếp điểm là \(x_0\Rightarrow4x_0^3+1=5\Rightarrow x_0^3=1\)
\(\Rightarrow x_0=1\Rightarrow y_0=2\)
Phương trình: \(y=5\left(x-1\right)+2\Leftrightarrow y=5x-3\)
33.
Vận tốc của chất điểm: \(v\left(t\right)=S'\left(t\right)=5-6t\)
\(v\left(t\right)=3\Rightarrow5-6t=3\Rightarrow t=\dfrac{1}{3}\)
\(\Rightarrow S=5.\dfrac{1}{3}-3.\left(\dfrac{1}{3}\right)^2=1,33\left(m\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2021
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4x+1}-\left(2x+1\right)+2x+1-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-\dfrac{4x^2}{\sqrt{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\left(-\dfrac{4}{\sqrt{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-4}{1+1}+\dfrac{12}{1+1+1}=2\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2021
\(f'\left(x\right)=\dfrac{1}{cos^2\left(x-\dfrac{2\pi}{3}\right)}\Rightarrow f'\left(0\right)=\dfrac{1}{cos^2\left(-\dfrac{2\pi}{3}\right)}=4\)
29 tháng 3 2021
\(y'=\left(m-1\right)\cos2x\cdot2-2\cdot\sin x-2m=0\)
\(\Leftrightarrow\left(m-1\right)\left(1-2\sin^2x\right)-\sin x-m=0\)
\(\Leftrightarrow2\left(1-m\right)\sin^2x-\sin x-1=0\)
bạn tự làm nốt nha
HT
9 tháng 3 2021
a/ \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt[3]{x^2-1}-2}{x-3}+\lim\limits_{x\rightarrow3}\dfrac{2-\sqrt[4]{1+5x}}{x-3}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x^2-1-8}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{16-1-5x}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4.\sqrt[3]{1+5x}+8\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{-5\left(x-3\right)}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4\sqrt[3]{1+5x}+8\right)}\)
\(=\dfrac{3+3}{\sqrt[3]{\left(3^2-1\right)^2}+2.\sqrt[3]{3^2-1}+4}-\dfrac{5}{\sqrt[4]{\left(1+5.3\right)^3}+2\sqrt[3]{\left(1+5.3\right)^2}+4.\sqrt[3]{1+5.3}+8}=\dfrac{11}{32}\)
\(\Rightarrow a^2+b^2=1145\)
HT
9 tháng 3 2021
40/
\(L=\lim\limits_{x\rightarrow0}\dfrac{af\left(x\right)+b^n-b^n}{f\left(x\right)\left[\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+....+b^{n-1}\right]}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+...+b^{n-1}}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{b^{n-1}+b^{n-1}++...+b^{n-1}}=\dfrac{a}{nb^{n-1}}\)
HP
9 tháng 12 2021
32.
Gọi T là biến cố "Trong 10 người được chọn có ít nhất 2 người là nữ".
\(\Rightarrow\overline{T}\) là biến cố "Trong 10 người được chọn không có quá 1 người là nữ"
\(\Rightarrow\left|\Omega\right|=C^{10}_{20}\)
TH1: Trong 10 người được chọn chỉ có 1 người là nữ.
\(\Rightarrow\) Có \(C^9_{12}.C^1_8\) cách chọn.
TH2: Cả 10 người được chọn đều là nam.
\(\Rightarrow\) Có \(C^{10}_{12}\) cách chọn.
\(\Rightarrow\left|\Omega_{\overline{T}}\right|=C^9_{12}.C^1_8+C^{10}_{12}\)
\(\Rightarrow P\left(\overline{T}\right)=\dfrac{\left|\Omega_{\overline{T}}\right|}{\left|\Omega\right|}=\dfrac{C^9_{12}.C^1_8+C^{10}_{12}}{C^{10}_{20}}=\dfrac{83}{8396}\)
\(\Rightarrow P\left(T\right)=1-P\left(\overline{T}\right)=\dfrac{8315}{8396}\)
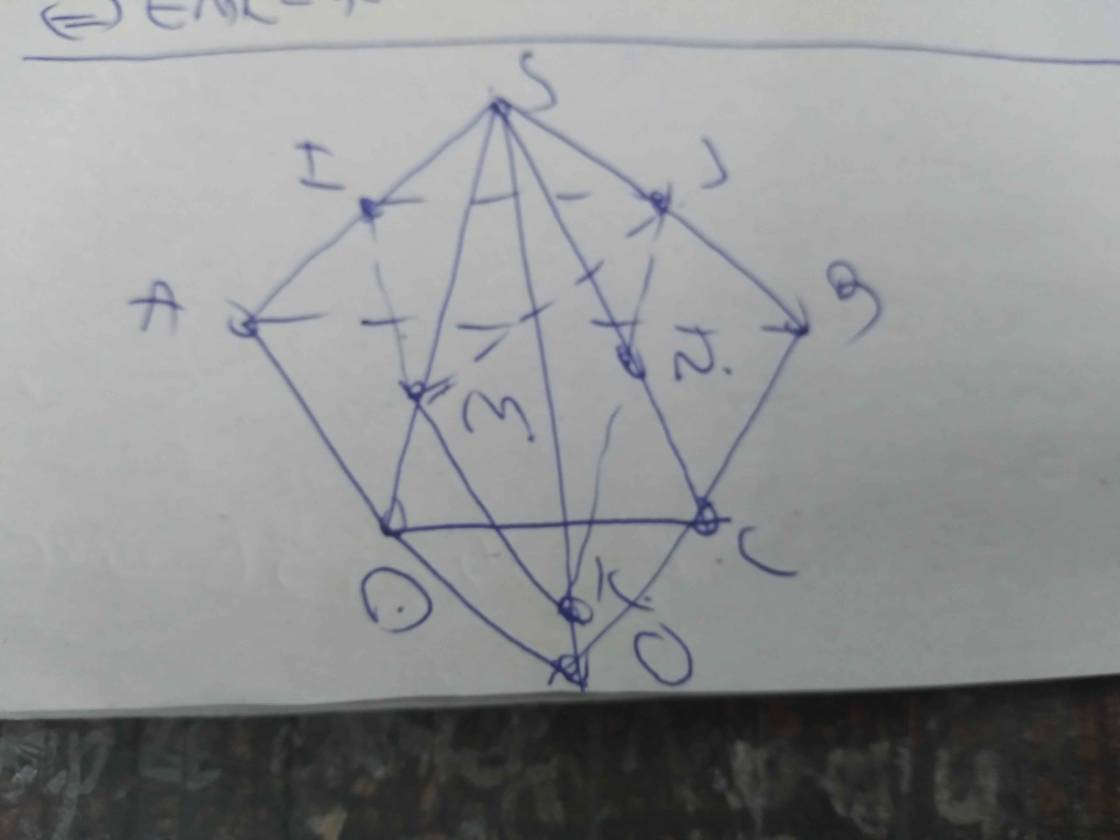
\(\left\{{}\begin{matrix}\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=0\\\overrightarrow{G_0B}+\overrightarrow{G_0C}+\overrightarrow{G_0D}=0\end{matrix}\right.\)
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{GG_0}+\overrightarrow{G_0A}\right)+\left(\overrightarrow{GG_0}+\overrightarrow{G_0B}\right)+\left(\overrightarrow{GG_0}+\overrightarrow{G_0C}\right)+\left(\overrightarrow{GG_0}+\overrightarrow{G_0D}\right)=\overrightarrow{0}\)
\(\Leftrightarrow4\overrightarrow{GG_0}+\overrightarrow{G_0A}+\left(\overrightarrow{G_0B}+\overrightarrow{G_0C}+\overrightarrow{G_0D}\right)=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{AG_0}=4\overrightarrow{GG_0}\)
\(\Rightarrow\overrightarrow{AG}+\overrightarrow{GG_0}=4\overrightarrow{GG_0}\)
\(\Rightarrow\overrightarrow{AG}=3\overrightarrow{GG_0}\)
\(\Rightarrow\overrightarrow{GA}=-3\overrightarrow{GG_0}\)