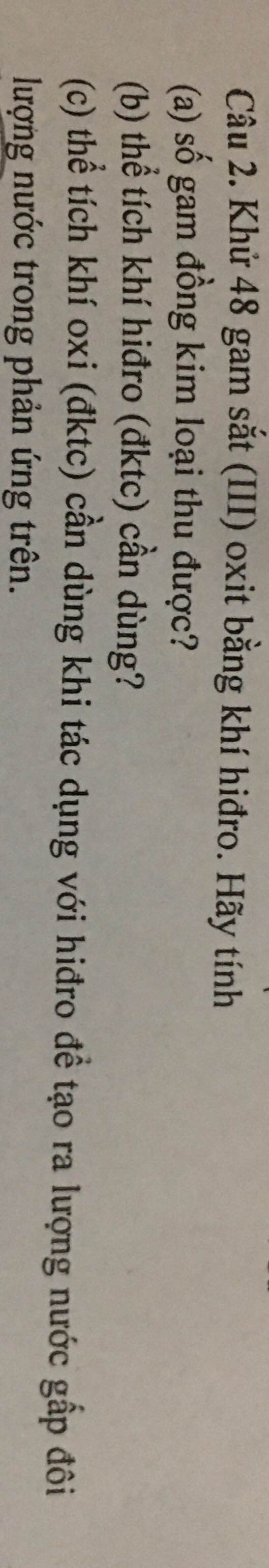NA
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PB
1
20 tháng 12 2022
\(m_{NaCl}=\dfrac{150.10}{100}=15\left(g\right)\\ m_{H_2O}=150-15=135\left(g\right)\)
Đong 15 gam NaCl khan, 135 gam nước cho sẵn vào cốc nước. Sau đó hóa tan 15 gam NaCl vào nước, dùng đũa thủy tinh khuấy đều thu được dd như theo yêu cầu của đề bài
17 tháng 3 2022
a.b.\(n_{Fe_2O_3}=\dfrac{48}{160}=0,3mol\)
\(Fe_2O_3+3H_2\rightarrow\left(t^o\right)2Fe+3H_2O\)
0,3 0,9 0,6 0,9 ( mol )
\(m_{Fe}=0,6.56=33,6g\)
\(V_{H_2}=0,9.22,4=20,16l\)
c.\(2H_2+O_2\rightarrow\left(t^o\right)2H_2O\)
0,9 1,8 ( mol )
\(V_{O_2}=0,9.22,4=20,16l\)
B
17 tháng 3 2022
câu 4
Zn+2Hcl->ZnCl2+H2
0,1--0,2---------------0,1
n Zn=\(\dfrac{6,5}{65}\)=0,1 mol
=>HCl dư
m HCl=0,05.36,5=1,825g
=>VH2=0,1.22,4=2,24l
bài5
4Al+3O2-to>2Al2O3
0,2----0,15
2KMnO4-to>K2MnO4+MnO2+O2
0,3-------------------------------------0,15
n Al=\(\dfrac{5,4}{27}\)=0,2 mol
VO2=0,15.22,4=3,36l
=>m KMnO4=0,3.158=47,4g
ND
1
MN
24 tháng 8 2021
\(2xR+yO_2\underrightarrow{^{^{t^0}}}2R_xO_y\)
\(2KMnO_4+16HCl_{\left(đ\right)}\underrightarrow{^{^{t^0}}}2KCl+2MnCl_2+5Cl_2+8H_2O\)
\(C_nH_{2n+2}+\dfrac{3n+1}{2}O_2\underrightarrow{^{^{t^0}}}nCO_2+\left(n+1\right)H_2O\)
\(8Al+30HNO_3\rightarrow8Al\left(NO_3\right)_3+3N_2O+15H_2O\)
TP
5 tháng 8 2021
a) \(M_X=M_{Br2}=160\) (đvC)
b) CT của hợp chất : X2O3
Ta có : \(2X+16.3=160\)
=> X=56
Vậy X là Fe
DT
Đỗ Thanh Hải
CTVVIP
27 tháng 4 2021
H2 + CuO \(\xrightarrow[]{t^o}\) Cu + H2O
a) nCuO = 16 : 80 = 0,2mol
Theo pt: nH2 = nCuO = 0,2 mol
=> V H2 = 0,2.22,4 = 4,48 lít
b) Theo pt: nCu = nCuO = 0,2 mol
=> mCu = 0,2 . 64 = 12,8g
nH2O = nCuO = 0,2 mol
=> mH2O = 0,2.18 = 3,6g
c) Fe + 2HCl \(\rightarrow\) FeCl2 + H2
Theo pt: nFe = nH2 = 0,2 mol
=> mFe = 0,2.56 = 11,2g
TP
2 tháng 12 2021
\(1.a.2Mg+O_2-^{t^o}\rightarrow2MgO\\ b.Fe+2AgNO_3\rightarrow Fe\left(NO_3\right)_2+2Ag\\ c.C_2H_4+3O_2-^{t^o}\rightarrow2CO_2+2H_2O\\ d.CuO+2HCl\rightarrow CuCl_2+H_2O\\ e.2Na+2H_2O\rightarrow2NaOH+H_2\\ f.4Al+3O_2-^{t^o}\rightarrow2Al_2O_3\)
TP
2 tháng 12 2021
\(2.a.Magie+Axitclohidric\rightarrow MagieClorua+Hidro\\ b.Mg+2HCl\rightarrow MgCl_2+H_2\\ c.m_{Mg}+m_{HCl}=m_{MgCl_2}+m_{H_2}\\ d.m_{HCl}=m_{MgCl_2}+m_{H_2}-m_{Mg}=47,5+1-12=36,5\left(g\right)\)
