
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=\left(3x^2-6x+3\right)-\left(x^2+2x+1\right)+2\left(x^2-9\right)-\left(4x^2+12x+9\right)-5+20x\)
\(=-30\)
b) \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x\left(x^2+4x+4\right)+\left(4x^2+4x+1\right)+\left(x^3-3x^2+9x+3x^2-9x+27\right)-1\)
\(=27\)
a: Ta có: \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=3x^2-6x+3-x^2-2x-1+2x^2-18-4x^2-12x-9-5+20x\)
\(=-30\)
b: Ta có: \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x^3-4x^2-4x+4x^2+4x+1+x^3+27-1\)
=27


2: \(A=x^2-10x+25-34=\left(x-5\right)^2-34\ge-34\forall x\)
Dấu '=' xảu ra khi x=5
\(1,C=x^2+x-3\\ \Rightarrow C=\left(x^2+x+\dfrac{1}{4}\right)-\dfrac{13}{4}\\ \Rightarrow C=\left(x+\dfrac{1}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\)
dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(C_{min}=-\dfrac{13}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
\(2,A=x^2-10x-9\\ \Rightarrow A=\left(x^2-10x+25\right)-34\\ \Rightarrow A=\left(x-5\right)^2-34\)
dấu "=" xảy ra \(\Leftrightarrow x=5\)
Vậy \(A_{min}=-34\Leftrightarrow x=5\)

a
vì ABC là tam giác cân=>góc B=C
vì P,Q là trung điểm AB,AC=>PQ là đường tb của tam giác ABC=>PQ//BC
vì PQ//BC=>BPQC là hình thang, mà góc B=C =>BPQC là hình thang cân
b
xét tứ giác ABCD có
Q là trung điểm BD,Q là trung điểm AC=>ABCD là hình bình hành

Bài `1`
\(a,A=a\left(a+b\right)-b\left(a+b\right)\\ =\left(a+b\right)\left(a-b\right)\)
Với `a=9;=10`
Ta có :
\(\left(a+b\right)\left(a-b\right)\\=\left(9+10\right)\left(9-10\right)\\ =19.\left(-1\right)\\ =-19\)
\(b,B=\left(3x+2\right)^2+\left(3x-2\right)^2-2\left(3x+2\right)\left(3x-2\right)\\ =\left(3x+2\right)^2-2\left(3x+2\right)\left(3x-2\right)+\left(3x-2\right)^2\\ =\left[\left(3x+2\right)-\left(3x-2\right)\right]^2\)
Với `x=-4`
Ta có :
\(\left[\left(3x+2\right)-\left(3x-2\right)\right]^2\\ =\left(3.4+2-3.4+2\right)^2\\ =\left(12+2-12+2\right)^2\\ =4^2\\ =16\)
\(2,\\ x^3-6x^2+9x\\ =x\left(x^2-6x+9\right)\\ =x\left(x-3\right)^2\\ x^2-2x-4y^2-4y\\ \)
`->` có đúng đề ko cậu
2:
b; x^2-4y^2-2x-4y
=(x-2y)*(x+2y)-2(x+2y)
=(x+2y)(x-2y-2)
a: x^3-6x^2+9x
=x(x^2-6x+9)
=x(x-3)^2

Mk ko ghi laj đề nha
\(=\left(17x^4:4x^2\right)-\left(5x^3:4x^2\right)+\left(2x^2:4x^2\right)\)
\(=\frac{17}{4}x^2-\frac{5}{4}x+\frac{2}{4}\)
\(=\frac{17}{4}x^2-\frac{5}{4}x+\frac{1}{2}\)
MK KO GHI LAJ ĐỀ NHA
\(=\left(17x^4:4x^2\right)-\left(5x^3:4x^2\right)+\left(2x^2:4x^2\right)\)
\(=\frac{17}{4}x^2-\frac{5}{4}x+\frac{1}{2}\)

Lời giải:
$MN\parallel BC$ nên:
$\widehat{M}+\widehat{B}=180^0$ (hai góc trong cùng phía)
$\widehat{M}+75^0=180^0$
$\widehat{M}=105^0$
$\widehat{N}+\widehat{C}=180^0$ (hai góc trong cùng phía)
$\widehat{N}+45^0=180^0$
$\widehat{N}=180^0-45^0=135^0$

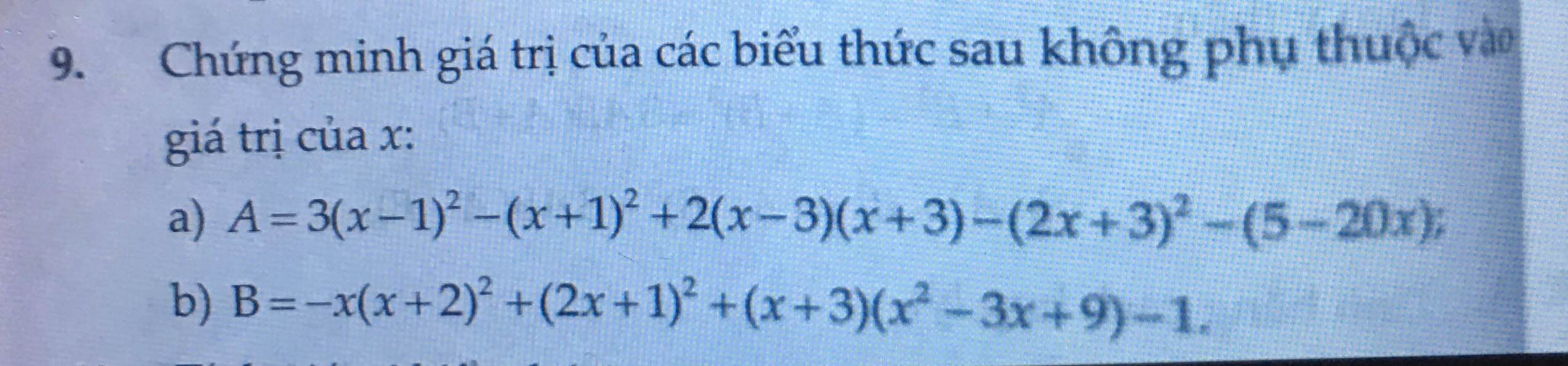

 đây bạn😀
đây bạn😀



a/ Ta có:
- ABCD là hình bình hành => \(AD=BC;AD\text{ // }BC\)
- Xét △ADH và △BKC có:
+ \(AD=BC\left(cmt\right)\)
+ \(\hat{ADH}=\hat{CBK}\left(slt\right)\)
=> \(\text{△ADH = △CBK}\left(c.h-g.n\right)\)
Vậy: \(...