
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
\(\dfrac{3}{4}+\dfrac{1}{4}:x=-3\)
\(\dfrac{1}{4}:x=-3-\dfrac{3}{4}\)
\(\dfrac{1}{4}:x=-\dfrac{15}{4}\)
\(x=\dfrac{1}{4}:\left(-\dfrac{15}{4}\right)\)
\(x=-\dfrac{1}{15}\)
b.
\(\dfrac{4}{7}x-x=\dfrac{-9}{14}\)
\(\Leftrightarrow\left(\dfrac{4}{7}-1\right)x=\dfrac{-9}{14}\)
\(\Leftrightarrow-\dfrac{3}{7}x=-\dfrac{9}{14}\)
\(\Leftrightarrow x=-\dfrac{9}{14}:\left(-\dfrac{3}{7}\right)\)
\(\Leftrightarrow x=\dfrac{3}{2}\)
c.
\(\dfrac{1}{2}x+\dfrac{3}{5}x=\dfrac{-2}{3}\)
\(\Leftrightarrow\left(\dfrac{1}{2}+\dfrac{3}{5}\right)x=-\dfrac{2}{3}\)
\(\Leftrightarrow\dfrac{11}{10}x=-\dfrac{2}{3}\)
\(\Leftrightarrow x=-\dfrac{2}{3}:\dfrac{11}{10}\)
\(\Leftrightarrow x=-\dfrac{20}{33}\)
Lời giải:
n. $\frac{1}{4}:x=-3-\frac{3}{4}=\frac{-15}{4}$
$x=\frac{1}{4}: \frac{-15}{4}=\frac{-1}{15}$
o.
$\frac{4}{7}x-x=\frac{-9}{14}$
$x(\frac{4}{7}-1)=\frac{-9}{14}$
$x.\frac{-3}{7}=\frac{-9}{14}$
$x=\frac{-9}{14}: \frac{-3}{7}=\frac{3}{2}$
p.
$\frac{1}{2}x+\frac{3}{5}x=\frac{-2}{3}$
$x(\frac{1}{2}+\frac{3}{5})=\frac{-2}{3}$
$x.\frac{11}{10}=\frac{-2}{3}$
$x=\frac{-2}{3}: \frac{11}{10}=\frac{-20}{33}$

-472 + (235 - 28) - 35 - 350
= -472 + 207 - 35 - 350
= -265 - 35 - 350
= 300 - 350 = -50

Bài làm của mk nek:
2x+3x=5
=> x.(2+3)=5
=> x.5=5
=> x=5:5
=> x=1

Lớp 6A có 48 học sinh gồm 3 loại : giỏi ,khá ,trung bình bt ¼ số học sinh của lớp là học sinh giỏi 2/3 số học sinh khá
a)tính số học sinh mỗi loại
b)tính tỉ số học sinh khá so với trung bình(viết kết quả dưới dạng số thập phân làm tròn đến hàng phần tram)?

a, \(\left(-2\right)^2-2x^2=-50.\)
\(\Leftrightarrow4-2x^2=-50\)
\(\Leftrightarrow2x^2-54=0\)
\(\Leftrightarrow x^2-27=0\)
\(\Leftrightarrow\left(x-3\sqrt{3}\right)\left(x+3\sqrt{3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=3\sqrt{3}\\x=-3\sqrt{3}\end{cases}}\)
\(\left(-2\right)^2-2x^2=-50\)
\(\Leftrightarrow x^2=\frac{-50-\left(-2\right)^2}{-2}\)
\(\Leftrightarrow x^2=27\)
\(\Leftrightarrow x=\pm\sqrt{27}\)
\(\Leftrightarrow x=\pm3\sqrt{3}\)
\(\frac{2}{x}-\frac{5}{x}=-9\)
\(\Leftrightarrow\frac{2-5}{x}=-9\)
\(\Leftrightarrow-3=-9x\)
\(\Leftrightarrow x=\frac{-3}{-9}=\frac{1}{3}\)

a: x-1 là bội của x+2
=>\(x-1⋮x+2\)
=>\(x+2-3⋮x+2\)
=>\(-3⋮x+2\)
=>\(x+2\inƯ\left(-3\right)\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)
b: 3x+1 là ước của x+2
=>\(x+2⋮3x+1\)
=>\(3x+6⋮3x+1\)
=>\(3x+1+5⋮3x+1\)
=>\(5⋮3x+1\)
=>\(3x+1\in\left\{1;-1;5;-5\right\}\)
=>\(3x\in\left\{0;-2;4;-6\right\}\)
=>\(x\in\left\{0;-\dfrac{2}{3};\dfrac{4}{3};-2\right\}\)
mà x nguyên
nên \(x\in\left\{0;-2\right\}\)
c: x+3 là ước của 2x+1
=>\(2x+1⋮x+3\)
=>\(2x+6-7⋮x+3\)
=>\(-7⋮x+3\)
=>\(x+3\in\left\{1;-1;7;-7\right\}\)
=>\(x\in\left\{-2;-4;4;-10\right\}\)
d: 3x+2 là bội của 2x-1
=>\(3x+2⋮2x-1\)
=>\(6x+4⋮2x-1\)
=>\(6x-3+7⋮2x-1\)
=>\(7⋮2x-1\)
=>\(2x-1\in\left\{1;-1;7;-7\right\}\)
=>\(2x\in\left\{2;0;8;-6\right\}\)
=>\(x\in\left\{1;0;4;-3\right\}\)

\(\frac{4}{x}=\frac{5-2y}{3}\Leftrightarrow x\left(5-2y\right)=12\)
Do \(x,y\)là số nguyên nên \(x,5-2y\)là các ước của \(12\)mà \(5-2y\)là số lẻ nên ta có bảng giá trị:
| 5-2y | 1 | 3 | -1 | -3 |
| x | 12 | 4 | -12 | -4 |
| y | 2 | 1 | 3 | 4 |
Vậy phương trình có các nghiệm là: \(\left(12,2\right),\left(4,1\right),\left(-12,3\right),\left(-4,4\right)\).

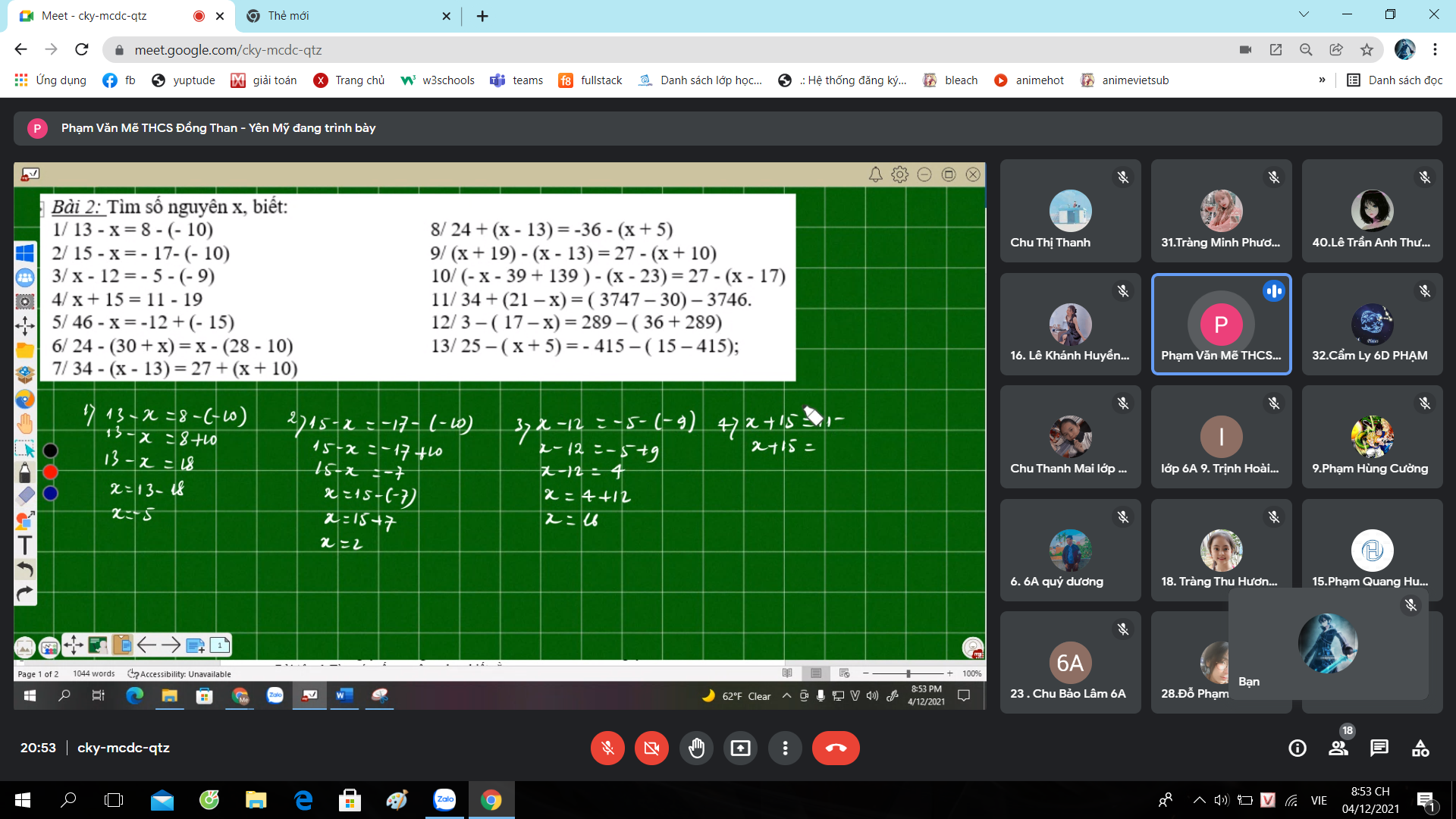
\(6,24-\left(30+x\right)=x-\left(28-10\right)\\ \Leftrightarrow24-30-x=x-18\\ \Leftrightarrow-6-x=x-18\\ \Leftrightarrow x-18+x+6=0\\ \Leftrightarrow2x-12=0\\ \Leftrightarrow2x=12\\ \Leftrightarrow x=6\)
6: \(\Leftrightarrow-6-x=x-18\)
\(\Leftrightarrow-2x=-12\)
hay x=6

`1
a)28 là bội của 7
b)14 là ước của 28
b)2 là ước của 28
c)0 là bội của 28
2)
42 ⋮ 7
42 ko cia hết cho 8
48 ko chia hết cho 15
48⋮ 16
3
trong 1 tổng,nếu mọi số hạng chia hết cho cùng 1 số thì tổng chia hết cho số đó
nếu trong 1 tổng chỉ có đúng 1 số ko chia cho một số,các số hạng còn lại đều chia hết cho số đó thì tổng ko chia hết cho số đó
4
a) Đ b) Đ
c) S d) Đ
5 D
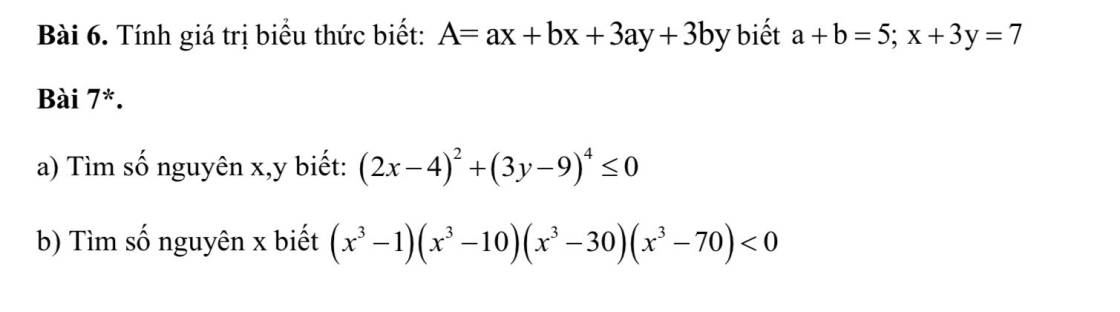
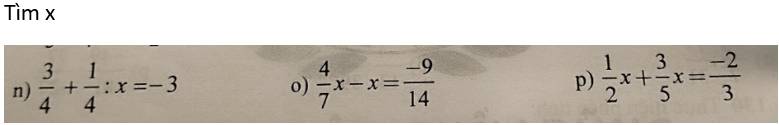 giupsp t voiii
giupsp t voiii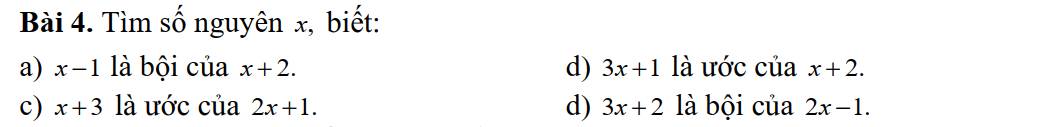

Bài 6:
\(A=ax+bx+3ay+3by\)
\(=x\left(a+b\right)+3y\left(a+b\right)\)
\(=\left(a+b\right)\left(x+3y\right)=5\cdot7=35\)
Bài 7:
a: \(\left(2x-4\right)^2>=0\forall x\)
\(\left(3y-9\right)^4>=0\forall y\)
Do đó: \(\left(2x-4\right)^2+\left(3y-9\right)^4>=0\forall x,y\)
mà \(\left(2x-4\right)^2+\left(3y-9\right)^4< =0\forall x,y\)
nên \(\left\{{}\begin{matrix}2x-4=0\\3y-9=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
b; (\(x^3\) - 1)(\(x^3\) - 10)(\(x^3\) - 30)(\(x^3\) - 70) < 0
Đặt \(x^3\) = t
Khi đó: T = (t - 1)(t - 10)(t - 30)(t - 70) < 0
Lập bảng xét dấu ta có:
Theo bảng trên ta có:
1 < t < 10 hoặc 30 < t < 70
⇒ 1 < \(x^3\) - 1 < 10 ⇒ 2 < \(x^3\) < 11
Vì \(x\) nguyên nên \(x\)3 = 8 ⇒ \(x^3\) = 23 ⇒ \(x=2\)
30 < t < 70
30 < \(x^3\) - 1 < 70
31 < \(x^3\) < 71
Vì \(x\) nguyên nên \(x^3\) = 64
⇒ \(x^3\) = 43 ⇒ \(x\) = 4
Vậy \(x\) \(\in\) {2; 4}