
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x\notin\left\{0;-1\right\}\)
Ta có: \(\dfrac{1}{x^2}+\dfrac{1}{\left(x+1\right)^2}=15\)
\(\Leftrightarrow\left(\dfrac{1}{x}\right)^2+\left(\dfrac{1}{x+1}\right)^2=15\)
\(\Leftrightarrow\left(\dfrac{1}{x}\right)^2+\left(\dfrac{1}{x+1}\right)^2-\dfrac{2}{x\left(x+1\right)}+\dfrac{2}{x\left(x+1\right)}=15\)
\(\Leftrightarrow\left(\dfrac{1}{x}-\dfrac{1}{x+1}\right)^2+\dfrac{2}{x\left(x+1\right)}=15\)
\(\Leftrightarrow\left(\dfrac{x+1}{x\left(x+1\right)}-\dfrac{x}{x\left(x+1\right)}\right)^2+\dfrac{2}{x\left(x+1\right)}=15\)
\(\Leftrightarrow\left(\dfrac{1}{x\left(x+1\right)}\right)^2+\dfrac{2}{x\left(x+1\right)}=15\)
\(\Leftrightarrow\dfrac{1}{x^2\cdot\left(x+1\right)^2}+\dfrac{2}{x\left(x+1\right)}-15=0\)(1)
Đặt \(\dfrac{1}{x\left(x+1\right)}=a\)(Điều kiện: \(x\notin\left\{0;-1\right\}\)
(1)\(\Leftrightarrow a^2+2a-15=0\)
\(\Leftrightarrow a^2+5a-3a-15=0\)
\(\Leftrightarrow a\left(a+5\right)-3\left(a+5\right)=0\)
\(\Leftrightarrow\left(a+5\right)\left(a-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+5=0\\a-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=-5\\a=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{x\left(x+1\right)}=-5\\\dfrac{1}{x\left(x+1\right)}=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\left(x+1\right)=-\dfrac{1}{5}\\x\left(x+1\right)=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+x+\dfrac{1}{5}=0\\x^2+x-\dfrac{1}{3}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{20}=0\\x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{7}{12}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{20}\\\left(x+\dfrac{1}{2}\right)^2=\dfrac{7}{12}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=\dfrac{\sqrt{5}}{10}\\x+\dfrac{1}{2}=-\dfrac{\sqrt{5}}{10}\\x+\dfrac{1}{2}=\dfrac{\sqrt{21}}{6}\\x+\dfrac{1}{2}=-\dfrac{\sqrt{21}}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-5+\sqrt{5}}{10}\left(nhận\right)\\x=\dfrac{-5-\sqrt{5}}{10}\left(nhận\right)\\x=\dfrac{-3+\sqrt{21}}{6}\left(nhận\right)\\x=\dfrac{-3-\sqrt{21}}{6}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{-5+\sqrt{5}}{10};\dfrac{-5-\sqrt{5}}{10};\dfrac{-3+\sqrt{21}}{6};\dfrac{-3-\sqrt{21}}{6}\right\}\)

Gọi x là qđ AB (km)
Vận tốc đi là \(25\left(\dfrac{km}{h}\right)\)
Vận tốc về là \(30\left(\dfrac{km}{h}\right)\)
Thời gian đi là \(\dfrac{x}{25}\left(h\right)\)
Thời gian về là \(\dfrac{x}{30}\left(h\right)\)
20p = 1/3(h)
Do thời gian về ít hơn lúc đi là 20p nên ta có
\(\dfrac{x}{25}-\dfrac{x}{30}=\dfrac{1}{3}\\ \Leftrightarrow30x-25x=\dfrac{1}{3}\\ \Leftrightarrow5x=\dfrac{1}{3}\\ \Leftrightarrow x=15\)
Cách giải đây nhé!
Gọi thời gian lúc đi là x(x>0) (h)
Đổi 20 phút = 1/3 giờ
Do thời gian về ít hơn thời gian đi là 20 phút nên thời gian lúc về là x−1/3
Do quãng đường không đổi nên ta có phương trình :
25x= 30(x−1/3)
⇔ 25x= 30x−10
⇔ −5x= −10


(x-1)/2015 + x/2014 + 1/503 - (x-3)/2013 - x/2012 - 1/1007 =0
(x-2016)/2015 + (x-2016)/2014 - (x-2016)/2012 - (x-2016)/2013 = 0
(x-2016) ( 1/2015 + 1/2016 - 1/2013 - 1/2012) = 0
Mà 1/2015 + 1/2016 - 1/2013 - 1/2012 khác 0
Suy ra x -2016=0
x=2016
Chỗ nào thắc mắc nhớ hỏi mik nhe!

Gọi số ngày theo kế hoạch sẽ hoàn thành xong là x
Theo đề, ta có phương trình:
40x+20=45x
=>-5x=-20
hay x=4
Vậy: Số sản phẩm đội phải thực hiện là 160 sản phẩm

Ta thấy : \(x^2+1\ge1\) nên để \(\left(3x-1\right)\left(x^2+1\right)< 0\)\(thì\) \(3x-1< 0\)\(hay\) \(x< \frac{1}{3}\)

bạn đăng tách ra nhé
Bài 3 :
Ta có :\(1+\dfrac{1}{2+x}=\dfrac{12}{x^3+8}\)
đk : x khác -2
\(\Rightarrow x^3+8+x^2-2x+4=12\Leftrightarrow x^3+x^2-2x=0\)
\(\Leftrightarrow x\left(x^2+x-2\right)=0\Leftrightarrow x\left(x-1\right)\left(x+2\right)=0\Leftrightarrow x=0;x=1;x=-2\left(ktm\right)\)
Bài 2:
a,ĐKXĐ:\(\left\{{}\begin{matrix}x\ne0\\x\ne2\end{matrix}\right.\)
\(\dfrac{1}{x}+\dfrac{2}{x-2}=0\\ \Leftrightarrow\dfrac{x-2}{x\left(x-2\right)}+\dfrac{2x}{x\left(x-2\right)}=0\\ \Leftrightarrow\dfrac{x-2+2x}{x\left(x-2\right)}=0\\ \Rightarrow3x-2=0\\ \Leftrightarrow x=\dfrac{2}{3}\left(tm\right)\)
b, ĐKXĐ:\(x\ne\pm2\)
\(\dfrac{x-1}{x+2}-\dfrac{x}{x-2}=\dfrac{5x-2}{4-x^2}\\ \Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2-5x}{x^2-4}\\ \Leftrightarrow\dfrac{x^2-3x+2-x^2-2x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2-5x}{\left(x-2\right)\left(x+2\right)}=0\\ \Leftrightarrow\dfrac{-5x+2-2+5x}{\left(x-2\right)\left(x+2\right)}=0\\ \Leftrightarrow0=0\left(tm\right)\)

bữa sau bạn nhớ giải thích nữa nha chớ mình không biết tại sao ra đáp án đó đâu

\(4+2x\left(2x+4\right)=-x\)
\(4+4x^2+8x=-x\)
\(4+4x^2+8x+x=0\)
\(4+4x^2+9x=0\)
=> vô nghiệm
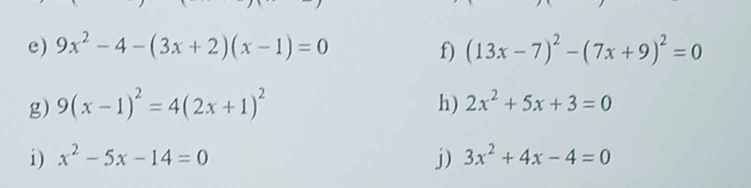



e.\(\Leftrightarrow9x^2-4-\left(3x^2-x-2\right)=0\)
\(\Leftrightarrow9x^2-4-3x^2+x+2=0\)
\(\Leftrightarrow6x^2+x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
f.\(\Leftrightarrow\left(13x-7\right)^2=\left(7x+9\right)^2\)
\(\Leftrightarrow13x-7=7x+9\)
\(\Leftrightarrow6x=16\Leftrightarrow x=\dfrac{16}{6}\)
g.\(\Leftrightarrow\left(9x-9\right)^2=\left(8x+4\right)^2\)
\(\Leftrightarrow9x-9=8x+4\)
\(\Leftrightarrow x=13\)
h.\(\Leftrightarrow2x^2+2x+3x+3=0\)
\(\Leftrightarrow2x\left(x+1\right)+3\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
i,\(\Leftrightarrow x^2+2x-7x-14=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=7\end{matrix}\right.\)
j.\(\Leftrightarrow\left(x-\dfrac{2}{3}\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-2\end{matrix}\right.\)