
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bữa sau bạn nhớ giải thích nữa nha chớ mình không biết tại sao ra đáp án đó đâu


e.\(\Leftrightarrow9x^2-4-\left(3x^2-x-2\right)=0\)
\(\Leftrightarrow9x^2-4-3x^2+x+2=0\)
\(\Leftrightarrow6x^2+x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
f.\(\Leftrightarrow\left(13x-7\right)^2=\left(7x+9\right)^2\)
\(\Leftrightarrow13x-7=7x+9\)
\(\Leftrightarrow6x=16\Leftrightarrow x=\dfrac{16}{6}\)
g.\(\Leftrightarrow\left(9x-9\right)^2=\left(8x+4\right)^2\)
\(\Leftrightarrow9x-9=8x+4\)
\(\Leftrightarrow x=13\)
h.\(\Leftrightarrow2x^2+2x+3x+3=0\)
\(\Leftrightarrow2x\left(x+1\right)+3\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
i,\(\Leftrightarrow x^2+2x-7x-14=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=7\end{matrix}\right.\)
j.\(\Leftrightarrow\left(x-\dfrac{2}{3}\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-2\end{matrix}\right.\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=AC/HA
=>AB*HA=HB*AC
b: AH=căn 5^2-3^2=4cm
BI là phân giác
=>HI/HB=IA/AB
=>HI/3=IA/5=(HI+IA)/(3+5)=0,5
=>HI=1,5cm; IA=1,5cm

1: \(=\dfrac{\dfrac{x^2+y^2-2xy}{xy}}{\dfrac{x^2-y^2}{xy}}\)
\(=\dfrac{\left(x-y\right)^2}{xy}:\dfrac{\left(x-y\right)\left(x+y\right)}{xy}=\dfrac{x-y}{x+y}\)
2: \(=\dfrac{x^2-1+x^2}{x\left(x+1\right)}:\dfrac{x^2-x^2+1}{x\left(x+1\right)}\)
\(=\dfrac{2x^2-1}{1}=2x^2-1\)

a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của BC
Do đó: DE là đường trung bình của ΔBAC
Suy ra: DE//AC
Xét tứ giác ACED có DE//AC
nên ACED là hình thang
mà \(\widehat{DAC}=90^0\)
nên ACED là hình thang vuông




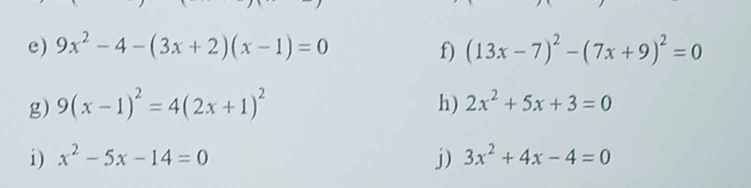
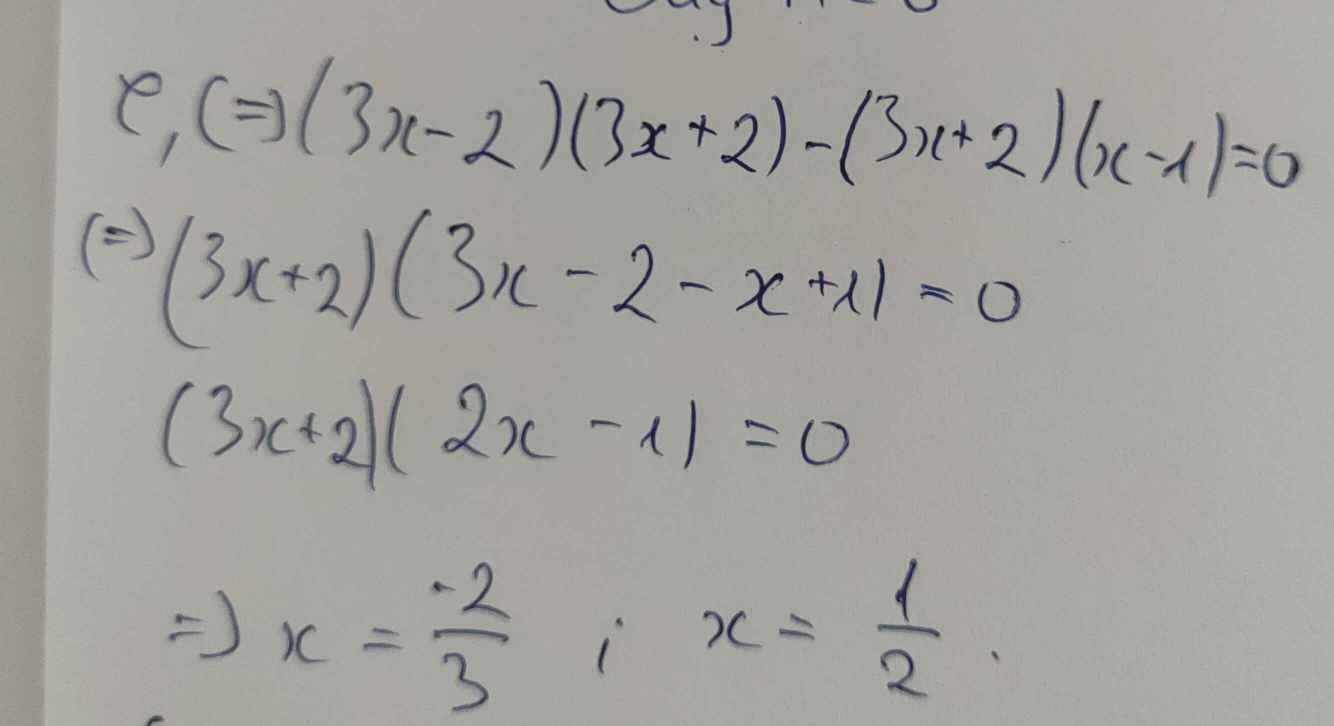
 vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều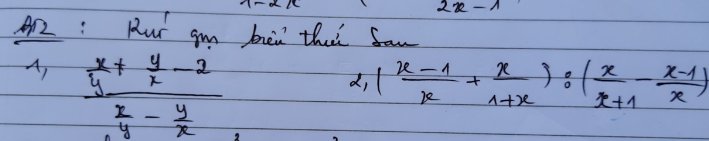
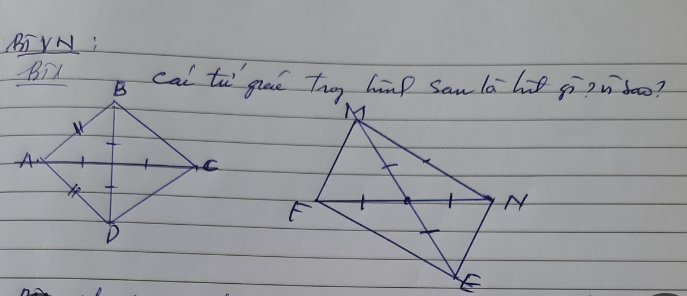
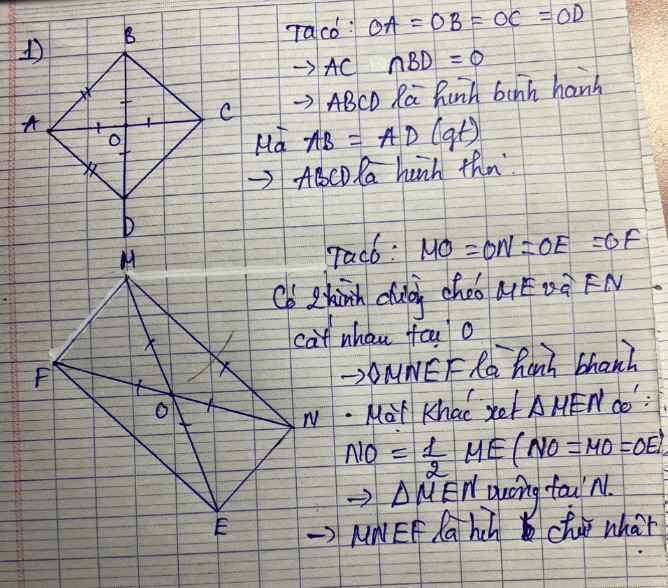
 giúp mik nha mn
giúp mik nha mn
\(A=\frac{x+\sqrt{7}}{x^2+2x\sqrt{7}+7}=\frac{x+\sqrt{7}}{x^2+2x\sqrt{7}+\left(\sqrt{7}\right)^2}=\frac{x+\sqrt{7}}{\left(x+\sqrt{7}\right)^2}=\frac{1}{x+\sqrt{7}}\)