
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


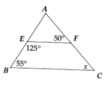
Xét tam giác ABC có:
\(\widehat{BEF}+\widehat{EBC}=125^0+55^0=180^0\)
Mà 2 góc này là 2 góc kề bù
=> EF//BC
=> \(\widehat{AFE}=\widehat{ACB}\)(2 góc đồng vị)
\(\Rightarrow x=50^0\)

\(a,\Rightarrow\left|\dfrac{7}{3}-\dfrac{3}{2}\right|-x=\dfrac{11}{2}-4\\ \Rightarrow x=\dfrac{11}{2}-\dfrac{5}{6}=\dfrac{14}{3}\\ b,\Rightarrow x+\dfrac{1}{2}=\dfrac{11}{2}-\dfrac{9}{2}=1\Rightarrow x=1-\dfrac{1}{2}=\dfrac{1}{2}\\ c,\Rightarrow x-2x+\dfrac{5}{2}=\dfrac{7}{4}\Rightarrow-x=\dfrac{7}{4}-\dfrac{5}{2}=-\dfrac{3}{2}\\ \Rightarrow x=\dfrac{3}{2}\)
a) \(\left|2\dfrac{1}{3}-1\dfrac{1}{2}\right|-x=3\dfrac{5}{2}-4\)
\(\Leftrightarrow\left|\dfrac{7}{3}-\dfrac{3}{2}\right|-x=\dfrac{11}{2}-4\)
\(\Leftrightarrow x=\dfrac{5}{6}-\dfrac{11}{2}+4\)
\(\Leftrightarrow x=-\dfrac{2}{3}\)
b) \(x+\left|-\dfrac{1}{2}\right|=3\dfrac{2}{3}-4\dfrac{1}{2}\)
\(\Leftrightarrow x+\dfrac{1}{2}=\dfrac{11}{3}-\dfrac{9}{2}\)
\(\Leftrightarrow x=\dfrac{11}{3}-\dfrac{9}{2}-\dfrac{1}{2}\Leftrightarrow x=-\dfrac{4}{3}\)
c) \(x-\left(2x-\dfrac{5}{2}\right)=\left|-\dfrac{7}{4}\right|\)
\(\Leftrightarrow x-2x+\dfrac{5}{2}=\dfrac{7}{4}\)
\(\Leftrightarrow-x=\dfrac{7}{4}-\dfrac{5}{2}\)
\(\Leftrightarrow-x=-\dfrac{3}{4}\Leftrightarrow x=\dfrac{3}{4}\)

\(2\left(2-x\right)\cdot2\cdot\left(2-x\right)\cdot1212\cdot\left(x-2\right)\cdot2\cdot\left(x-2\right)\cdot2=0\)
\(4\left(2-x\right)^2\cdot4848\left(x-2\right)^2=0\)
\(19392\left(2-x\right)^2\left(x-2\right)^2=0\)
\(\left(2-x\right)^2\left(x-2\right)^2=0\)
\(TH1:\left(2-x\right)^2=0\Rightarrow2-x=0\Rightarrow x=2\)
\(TH2:\left(x-2\right)^2=0\Rightarrow x-2=0\Rightarrow x=2\)
Vậy x = 2
<br class="Apple-interchange-newline"><div id="inner-editor"></div>2(2−x)·2·(2−x)·1212·(x−2)·2·(x−2)·2=0
4(2−x)2·4848(x−2)2=0
19392(2−x)2(x−2)2=0
(2−x)2(x−2)2=0
TH1:(2−x)2=0⇒2−x=0⇒x=2
TH2:(x−2)2=0⇒x−2=0⇒x=2
x = 2

Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$

ok nhưng mình không biết bạn ý ở đâu ! cậu nói thì mình mới k ! cho cả 4 k luôn ! nhưng chỉ cần cậu nói cho mình biết cậu ý ở đâu và cậu phải nhớ k cho mình thì mình mới k được chứ ! đồng ý hông ? đồng ý thì k mình 1 k trước !
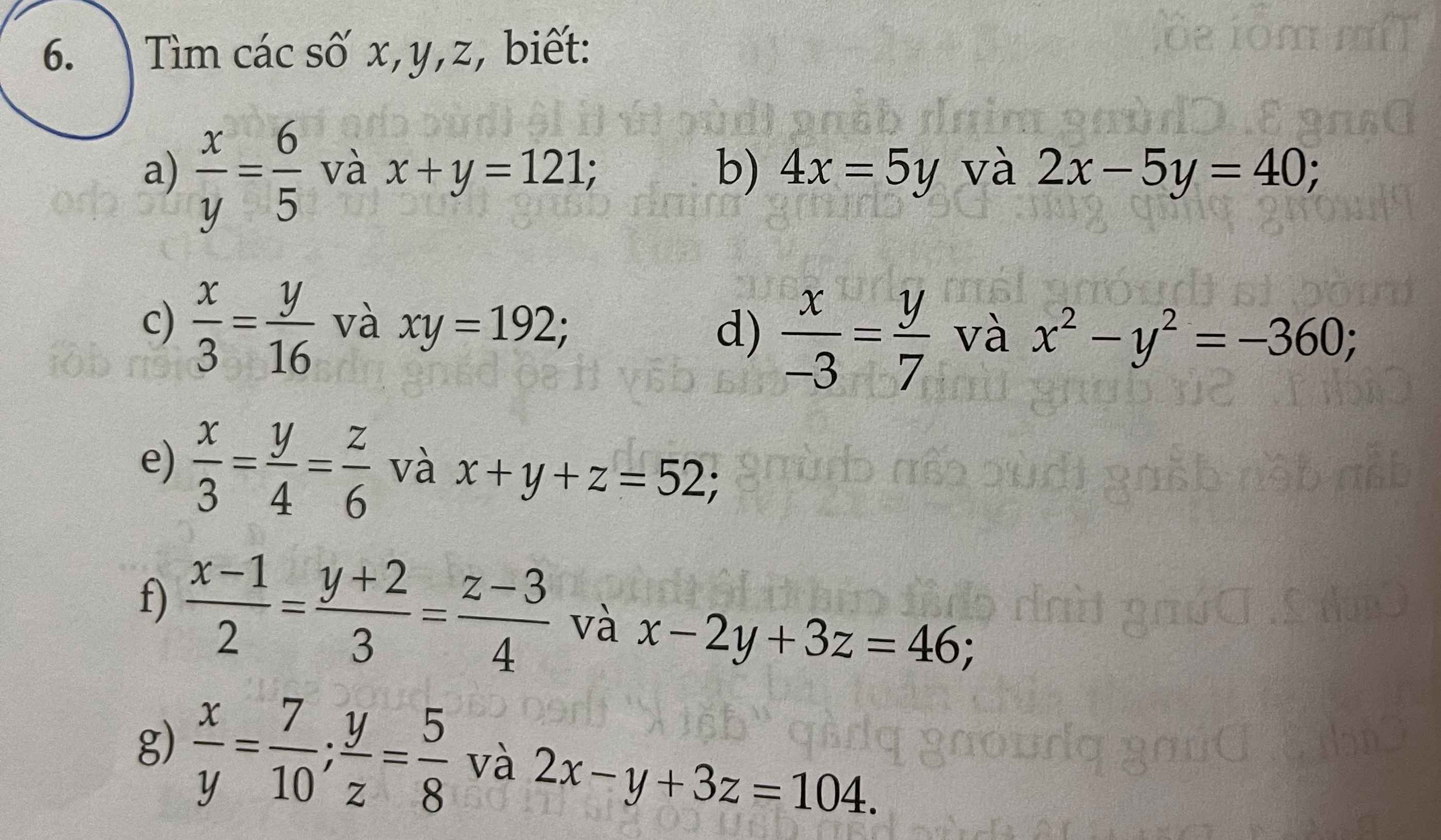
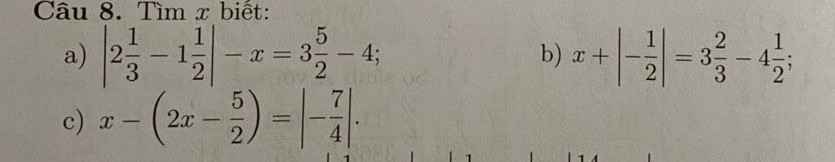




\(\dfrac{x}{y}=\dfrac{6}{5}\)⇒\(\dfrac{x}{6}=\dfrac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{x+y}{6+5}=\dfrac{121}{11}=11\)
⇒\(x=66;y=55\)
các bạn giải rõ giúp mik nha! rùi mik tik cho, :3