Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

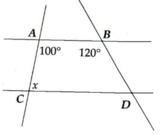
\(a//b\) nên \(\widehat{CAB}+\widehat{ACD}=180^0\left(2.góc.trong.cùng.phía\right)\)
Hay \(x+100^0=180^0\Rightarrow x=80^0\)

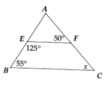
Ta có \(\widehat{FEB}+\widehat{EBC}=125^0+55^0=180^0\)
Mà 2 góc này ở vị trí trong cùng phía nên \(EF//BC\)
Do đó \(\widehat{AFE}=\widehat{ACB}=50^0\)(2 góc đồng vị)
\(\Rightarrow x=\widehat{ACB}=50^0\)

Vì \(AB//CD\) nên \(\widehat{BAC}+\widehat{CAD}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{CAD}=180^0-\widehat{BAC}=180^0-100^0=80^0\\ \Rightarrow x=80^0\)
Ta có: a//b(gt)
\(\Rightarrow\widehat{BAC}+\widehat{ACD}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{ACD}=180^0-\widehat{BAC}\)
\(\Rightarrow x=180^0-100^0=80^0\)


\(\left|x+1\right|và\left|x+2\right|\ge0\)
\(\Rightarrow\orbr{\begin{cases}\left(x+1\right)+\left(x+2\right)=3\\\left(x+1\right)+\left(x+2\right)=-3\end{cases}}\)
\(\orbr{\begin{cases}2x+3=3\\2x+3=-3\end{cases}}\)
\(\orbr{\begin{cases}2x=0\\2x=-6\end{cases}}\)
\(\orbr{\begin{cases}x=0\\x=-3\end{cases}}\)
\(\left|x+1\right|+\left|x+2\right|=3\)
Xét \(x+1\ge0;x+2\ge0\Leftrightarrow x\ge-1;x\ge-2\Rightarrow x\ge-1\) ta có : \(\hept{\begin{cases}\left|x+1\right|=x+1\\\left|x+2\right|=x+2\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|=3\Leftrightarrow x+1+x+2=3\Leftrightarrow2x+3=3\Rightarrow x=0\)(TM)
Xét \(x+1\le0;x+2\ge0\Leftrightarrow-2\le x\le-1\) ta có : \(\hept{\begin{cases}\left|x+1\right|=-x-1\\\left|x+2\right|=x+2\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|=3\Leftrightarrow-x-1+x+2=3\Leftrightarrow1=3\) (loại)
Xét \(x+1\le0;x+2\le0\Leftrightarrow x\le-1;x\le-2\Leftrightarrow x\le-2\) ta có : \(\hept{\begin{cases}\left|x+1\right|=-x-1\\\left|x+2\right|=-x-2\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|=-x-1-x-2=-2x-3=3\Rightarrow x=-3\)(TM)
Vậy \(x=\left\{-3;0\right\}\)

Xét tam giác ABC có:
\(\widehat{BEF}+\widehat{EBC}=125^0+55^0=180^0\)
Mà 2 góc này là 2 góc kề bù
=> EF//BC
=> \(\widehat{AFE}=\widehat{ACB}\)(2 góc đồng vị)
\(\Rightarrow x=50^0\)
Đúng nè