Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Áp dụng định lí pytago trong \(\Delta MNP\) vuông tại \(M\) có:
\(\Rightarrow MP=\sqrt{NP^2-MN^2}=\sqrt{7,5^2-4,5^2}=6cm\)
\(\Rightarrow D\)

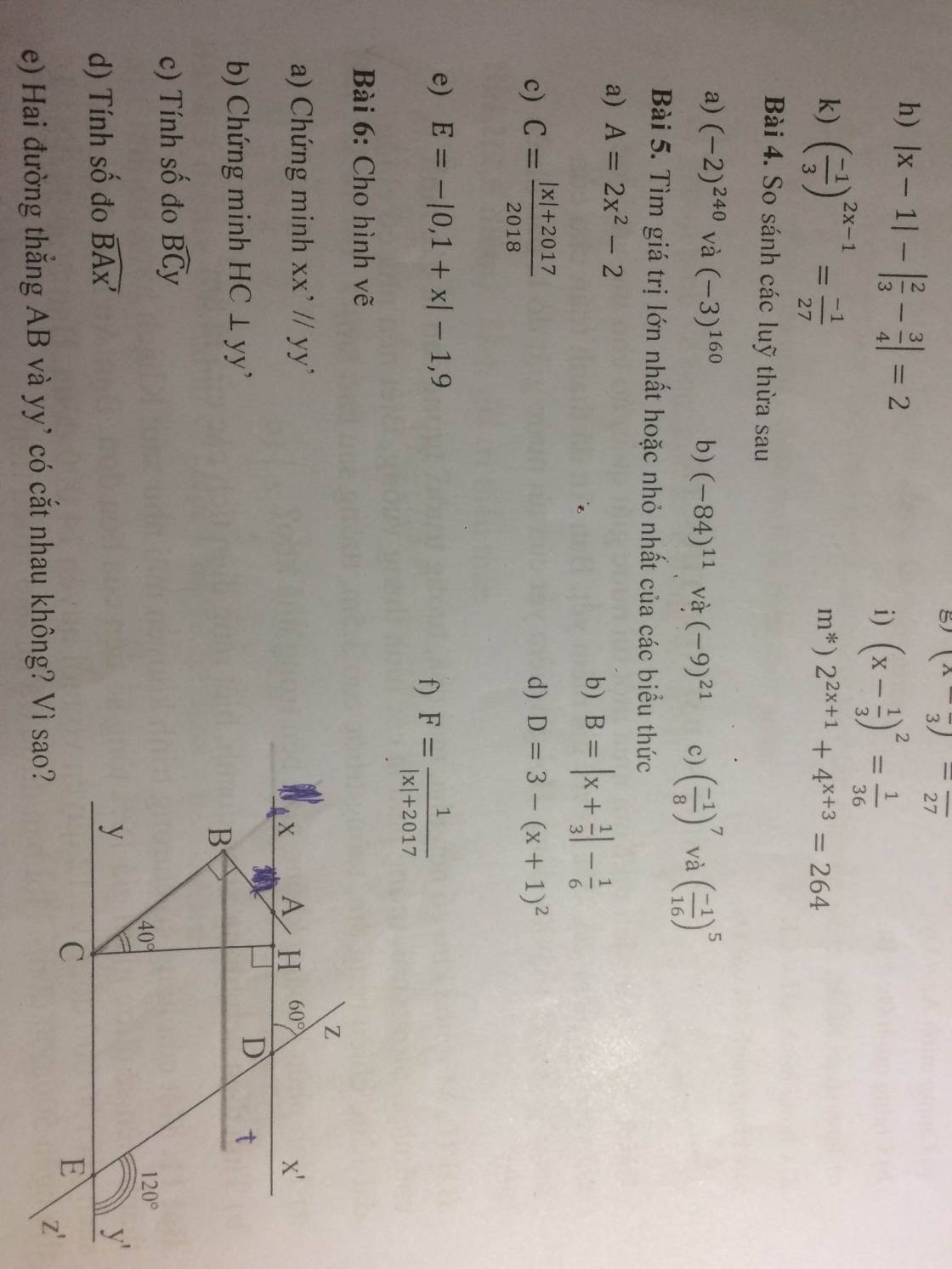
a) ∠CEz + ∠zEy' = 180⁰ (kề bù)
⇒ ∠CEz = 180⁰ - ∠zEy'
= 180⁰ - 120⁰
= 60⁰
⇒ ∠CEz = ∠xDz = 60⁰
Mà ∠CEz và ∠xDz là hai góc đồng vị
⇒ xx' // yy'
b) Do HC ⊥ xx' (gt)
xx' // yy' (cmt)
⇒ HC ⊥ yy'
c) Do HC ⊥ yy' (cmt)
⇒ ∠HCy = 90⁰
⇒ ∠BCy = ∠HCy - ∠BCH
= 90⁰ - 40⁰
= 50⁰
c) Vẽ tia Bt // xx'//yy'
⇒ ∠CBt = ∠BCy = 50⁰ (so le trong)
⇒ ∠ABt = ∠ABC - ∠CBt
= 90⁰ - 50⁰
= 40⁰
Do Bt // xx'
⇒ ∠xAB = ∠ABt = 40⁰ (so le trong)
Ta có:
∠BAx' + ∠xAB = 180⁰ (kề bù)
⇒ ∠BAx' = 180⁰ - ∠xAB
= 180⁰ - 40⁰
= 140⁰
e) Do AB cắt tia Bt tại B
Mà Bt // yy'
⇒ AB cắt yy'


OM\(\perp\)AB
=>\(\widehat{MOA}=\widehat{MOB}=90^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\widehat{AOE}< \widehat{AOM}\)
nên tia OE nằm giữa hai tia OA và OM
=>\(\widehat{AOE}+\widehat{MOE}=\widehat{AOM}=90^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OB, ta có: \(\widehat{BOF}< \widehat{BOM}\)
nên tia OF nằm giữa hai tia OB và OM
=>\(\widehat{BOF}+\widehat{MOF}=\widehat{BOM}=90^0\)
=>\(\widehat{AOE}+\widehat{MOE}=\widehat{BOF}+\widehat{MOF}\)
mà \(\widehat{AOE}=\widehat{BOF}\)
nên \(\widehat{MOE}=\widehat{MOF}\)
=>OM là phân giác của \(\widehat{EOF}\)