
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


C nguyên
=>2căn x+2+3 chia hết cho căn x+1
=>căn x+1 thuộc Ư(3)
=>căn x+1=1 hoặc căn x+1=3
=>x=4 hoặc x=0

a) xét delta phẩy ta có b'2 - ac
<=> 4 - m
b) để pt 1 luôn có nghiệm thì delta phẩy ≥ 0
=> 4-m ≥ 0 => m ≤ 4
c) xét delta phẩy của pt (1) ta có
4 - m để pt có 2 nghiệm x1,x2 thì delta phẩy ≥ 0 => m ≤ 4
theo Vi-ét ta có:\(\left\{{}\begin{matrix}x1+x2=4\\x1x2=m\end{matrix}\right.\)
theo bài ra ta có: x12 + x22 = 12 <=> ( x1+x2 )2 - 2x1x2 = 12
<=> 16 - 2m -12 = 0 <=> 2m = 4 <=> m = 2 ( thỏa đk)
vậy m = 2 thì pt thỏa mãn điều kiện.
d) A= x12 + x22
<=> A = (x1+x2)2 - 2x1x2
<=> A = 16 - 2m ta có m ≤ 4
nên giá trị lớn nhất của m = 4
vậy giá trị nhỏ nhất của A = 16 - 2.4
GTNN của A = 8 dấu "=" xảy ra khi m = 4
a) Ta có: a = 1 ; b' = -2 ; c = m
⇒ △' = b'2 - ac = ( -2 )2 - 1 .m = 4 - m
b) Để phương trình luôn có nghiệm thì △' \(\ge\) 0
⇒ 4 - m \(\ge\) 0 ⇔ m \(\le\) 4
Vậy khi m \(\le\) 4 thì phương trình luôn có nghiệm
c) Theo câu (b) thì phương trình luôn có nghiệm khi m \(\le\) 4
Theo hệ thức Vi - ét ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=4\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)
Do đó:
\(x_1^2+x_2^2=12\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=12\)
\(\Leftrightarrow4^2-2m=12\)
\(\Leftrightarrow4=2m\Leftrightarrow m=2\)
Vậy khi m = 2 thì phương trình (1) có 2 nghiệm x1 ; x2 thỏa mãn x12 + x22 = 12

\(\widehat{E}=180^0-\left(\widehat{D}+\widehat{F}\right)=41^0\)
Trong tam giác vuông DEH:
\(cotE=\dfrac{EH}{DH}\Rightarrow EH=DH.cotE\)
Trong tam giác vuông DFH:
\(cotF=\dfrac{FH}{DH}\Rightarrow FH=DH.cotF\)
\(\Rightarrow EH+FH=\text{DH}.cotE+DH.cotF\)
\(\Leftrightarrow EF=DH\left(cotE+cotF\right)\)
\(\Rightarrow DH=\dfrac{EF}{cotE+cotF}=\dfrac{15}{cot41^0+cot24^0}\approx4,42\left(cm\right)\)
Trong tam giác vuông DEH
\(sinE=\dfrac{DH}{DE}\Rightarrow DE=\dfrac{DH}{sinE}=\dfrac{4,42}{sin41^0}\approx6,74\left(cm\right)\)


=\(\sqrt{2\left(12-6\sqrt{3}\right)}-\sqrt{2\left(28+10\sqrt{3}\right)}\)
=\(\sqrt{2\left(3-\sqrt{3}\right)2}-\sqrt{2\left(5+\sqrt{3}\right)^2}\)
=\(\sqrt{2}\left(3-\sqrt{3}\right)-\sqrt{2}\left(5+\sqrt{3}\right)=\sqrt{2}\left(3-\sqrt{3}-5-\sqrt{3}\right)\)
=\(\sqrt{2}\left(-2-2\sqrt{3}\right)\)=\(-2\sqrt{2}-2\sqrt{6}\)

\(x^2+7x=810\)
\(\Leftrightarrow\left(x^2+2\cdot\frac{7}{2}\cdot x+\frac{49}{4}\right)=810+\frac{49}{4}\)
\(\Leftrightarrow\left(x+\frac{7}{2}\right)^2=\frac{3289}{4}\)
\(\Leftrightarrow\orbr{\begin{cases}x+\frac{7}{2}=\frac{\sqrt{3289}}{2}\\x+\frac{7}{2}=\frac{-\sqrt{3289}}{2}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{\sqrt{3289}-7}{2}\\x=\frac{-\sqrt{3289}-7}{2}\end{cases}}\)

Áp dụng BĐT bunniacoxki ta có:
\(\left(b^2+\left(c+a\right)^2\right)\left(1+4\right)\ge\left(b+2\left(a+c\right)\right)^2\)
=> \(\sqrt{\frac{a^2}{b^2+\left(c+a\right)^2}}\le\sqrt{5}.\frac{a}{b+2c+2a}\)
=> \(VT\le\sqrt{5}.\left(\frac{a}{b+2c+2a}+\frac{b}{c+2a+2b}+\frac{c}{a+2b+2c}\right)\)
Cần CM \(\frac{a}{b+2c+2a}+\frac{b}{c+2a+2b}+\frac{c}{a+2b+2c}\le\frac{3}{5}\)
<=>\(\left(\frac{1}{2}-\frac{a}{b+2c+2a}\right)+\left(\frac{1}{2}-\frac{b}{c+2a+2b}\right)+\left(\frac{1}{2}-\frac{c}{a+2b+2c}\right)\ge\frac{9}{10}\)
<=>\(\frac{b+2c}{b+2c+2a}+\frac{c+2a}{c+2a+2b}+\frac{a+2b}{a+2b+2c}\ge\frac{9}{5}\)
Áp dụng bđt buniacoxki dạng phân thức ở vế trái:
=> \(VT\ge\frac{\left(b+2c+c+2a+a+2b\right)^2}{\left(b+2c\right)^2+2a\left(b+2c\right)+\left(c+2a\right)^2+2b\left(c+2a\right)+\left(a+2b\right)^2+2c\left(a+2b\right)}\)
\(=\frac{9\left(a+b+c\right)^2}{5\left(a+b+c\right)^2}=\frac{9}{5}\)(ĐPCM)
Dấu bằng xảy ra khi a=b=c

a: góc AEH=1/2*180=90 độ
=>HE vuông góc AB
góc AFH=1/2*180=90 độ
=>HF vuông góc AC
Vì góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
b: AEHF làhình chữ nhật
=>góc AFE=góc AHE=góc B
=>góc B+góc FCB=180 độ
=>BEFC nội tiếp

\(=\dfrac{1}{\sqrt{x}+1}-\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1-x-\sqrt{x}}{x-1}=\dfrac{-x-1}{x-1}\)

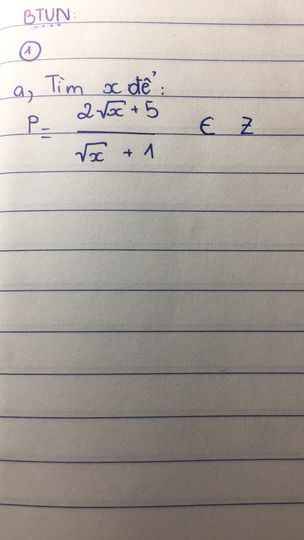
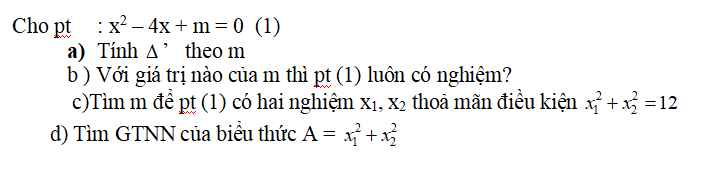 giúp mình với ạ.Mình cần lời giải chi tiết
giúp mình với ạ.Mình cần lời giải chi tiết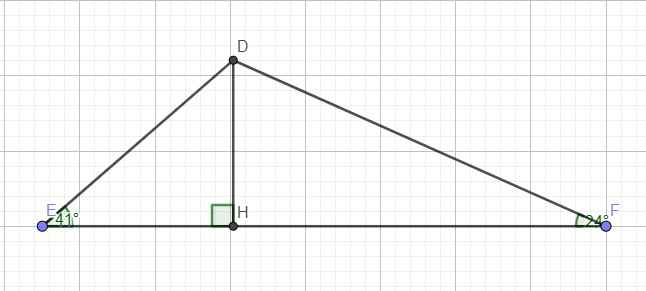

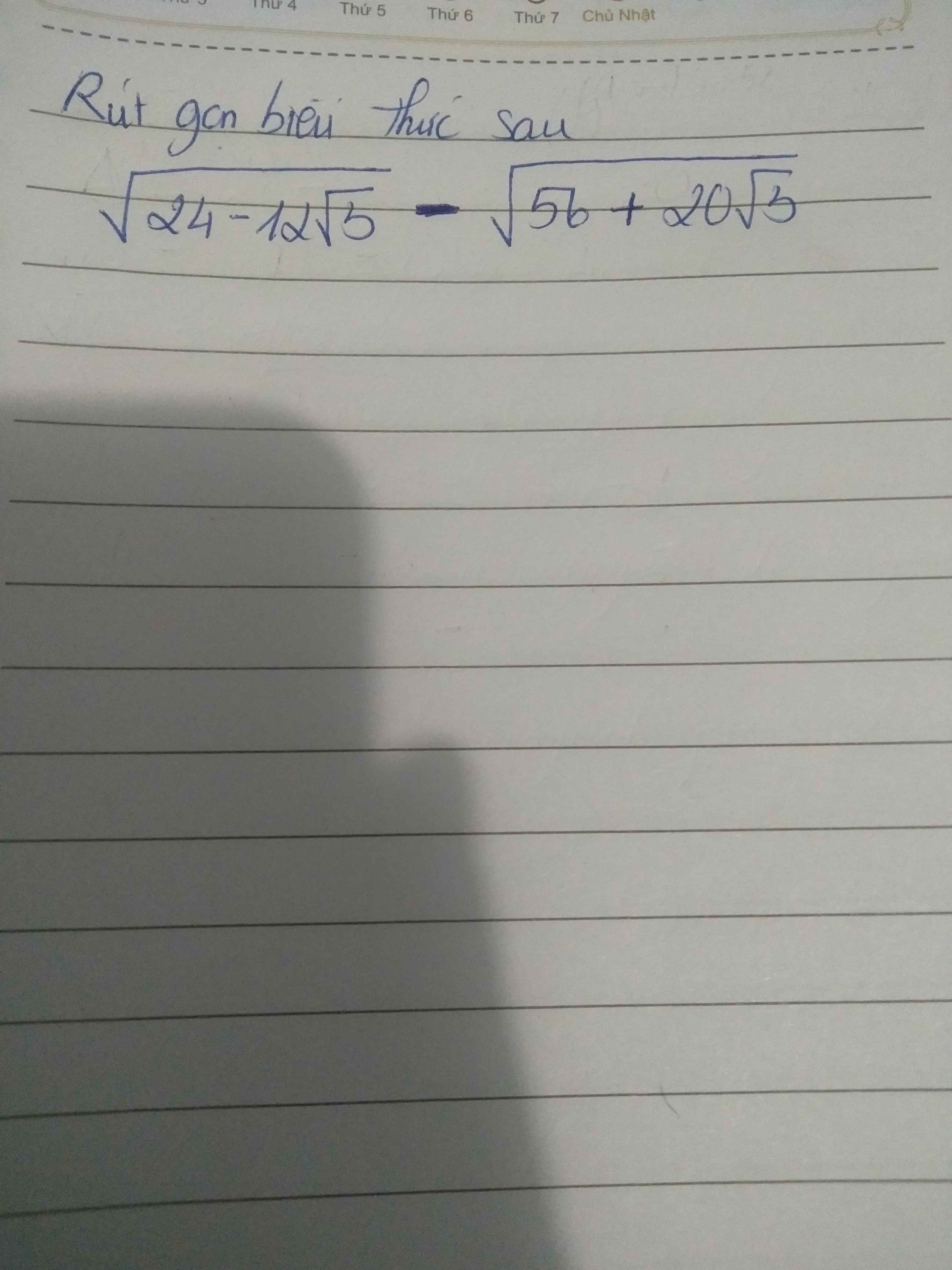
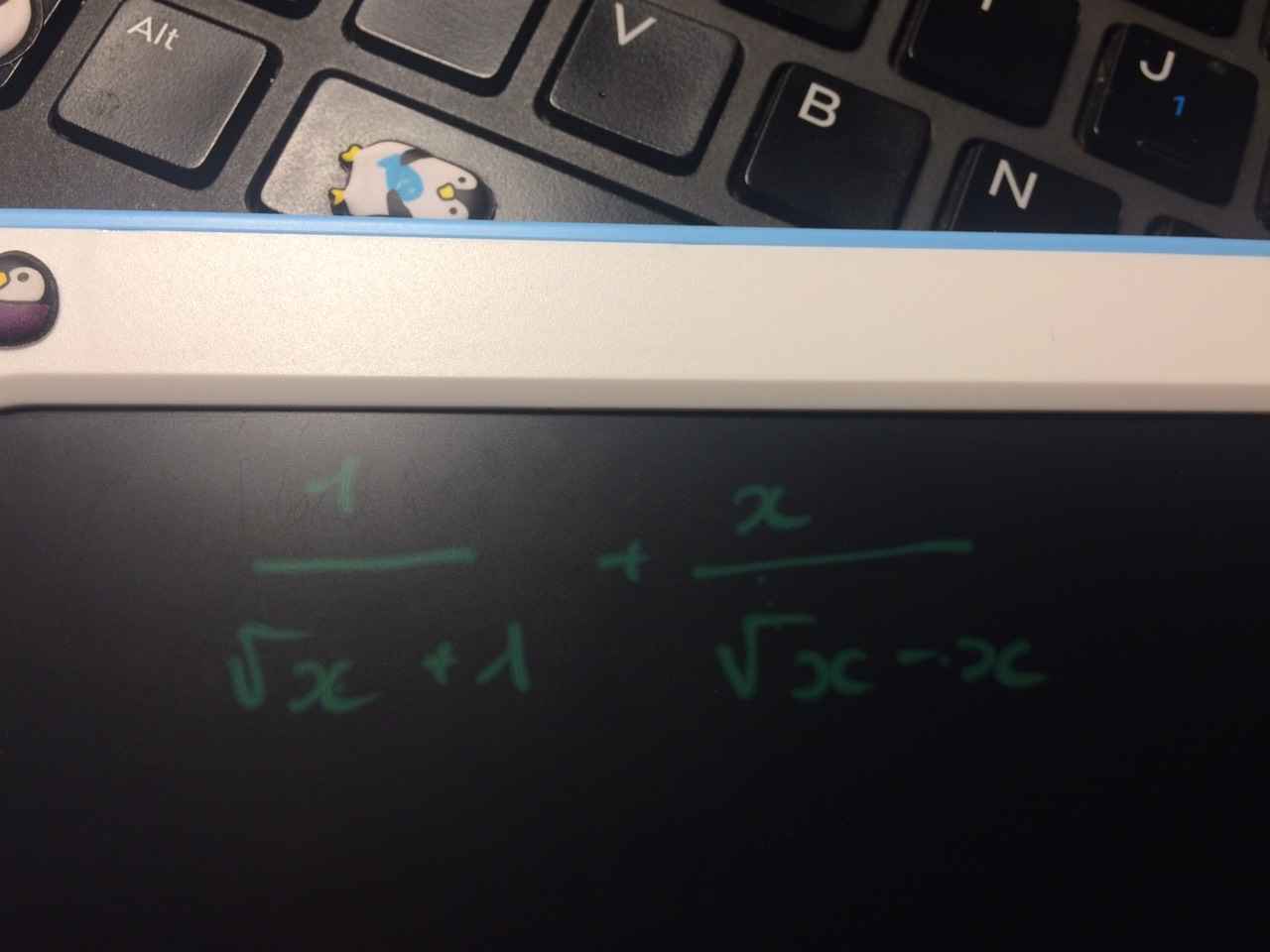
1.\(x=4-2\sqrt{3}-\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2=\left(\sqrt{3}-1\right)^2\)
\(A=\dfrac{2x-3\sqrt{x}-2}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)\left(2\sqrt{x}+1\right)}{\sqrt{x}-2}=2\sqrt{x}+1=2\sqrt{\left(\sqrt{3}-1\right)^2}+1=2\left(\sqrt{3}-1\right)+1=2\sqrt{3}-2+1=2\sqrt{3}-1\)
2.\(B=\dfrac{\sqrt{x^3}-\sqrt{x}+2x-2}{\sqrt{x}+2}=\dfrac{\sqrt{x}^2\left(\sqrt{x}+2\right)-\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}+2\right)\left(x-1\right)}{\sqrt{x}+2}=x-1\)
\(B=A+1\)
\(\Leftrightarrow x-1=2\sqrt{x}+1+1\)
\(\Leftrightarrow x-1=2\sqrt{x}+2\)
\(\Leftrightarrow x-2x\sqrt{x}-3=0\)
\(\Leftrightarrow\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=-1\left(vô.lý\right)\end{matrix}\right.\) \(\rightarrow x=\sqrt{3}\)