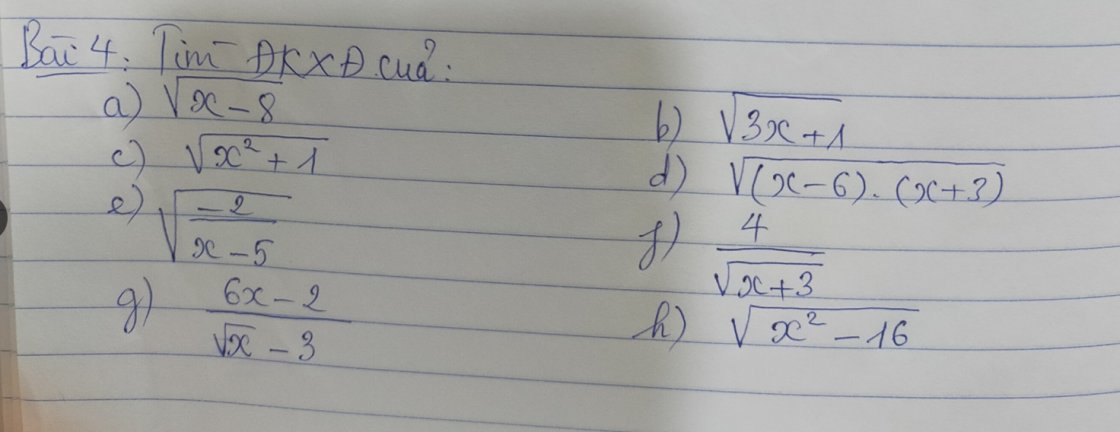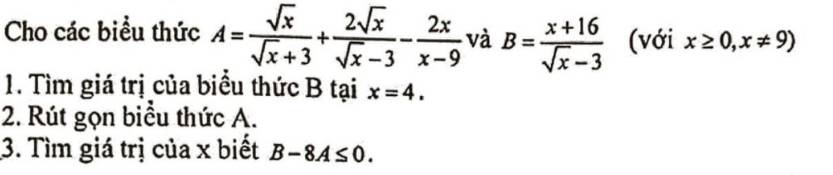K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
không cần làm câu c đâu ạ, giúp e với nhaaa mn
1
31 tháng 12 2021
Bài 2:
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
VT
không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
1
28 tháng 10 2021
\(2,\Leftrightarrow\left\{{}\begin{matrix}20x+25y-10xy=0\\20x-30y+xy=0\end{matrix}\right.\Leftrightarrow55y-11xy=0\\ \Leftrightarrow11y\left(5-x\right)=0\Leftrightarrow\left[{}\begin{matrix}y=0\\x=5\end{matrix}\right.\)
Với \(y=0\Leftrightarrow4x+0=0\Leftrightarrow x=0\)
Với \(x=5\Leftrightarrow20+5y=10y\Leftrightarrow y=4\)
Vậy \(\left(x;y\right)=\left\{\left(0;0\right);\left(5;4\right)\right\}\)
H9
HT.Phong (9A5)
CTVHS
17 tháng 7 2023
a) \(\sqrt{x-8}\) xác định khi
\(x-8\ge0\Leftrightarrow x\ge8\)
b) \(\sqrt{3x+1}\) xác định khi
\(3x+1\ge0\Leftrightarrow3x\ge-1\Leftrightarrow x\le-\dfrac{1}{3}\)
c) \(\sqrt{x^2+1}\)
Ta có: \(x^2\ge0\Rightarrow x^2+1\ge0\)
Vậy biểu thức được xác định với mọi x
d) \(\sqrt{\left(x-6\right)\left(x+3\right)}\)
Xác định khi
\(\left\{{}\begin{matrix}\left\{{}\begin{matrix}x-6\ge0\\x+3\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-6< 0\\x+3\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}x\ge6\\x\ge-3\end{matrix}\right.\\\left\{{}\begin{matrix}x< 6\\x< -3\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge6\\x< -3\end{matrix}\right.\)
H9
HT.Phong (9A5)
CTVHS
17 tháng 7 2023
e) \(\sqrt{\dfrac{-2}{x-5}}\) xác định khi
\(\left\{{}\begin{matrix}\dfrac{-2}{x-5}\ge0\\x-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le5\\x\ne5\end{matrix}\right.\)
\(\Leftrightarrow x< 5\)
f) \(\dfrac{4}{\sqrt{x+3}}\) xác định khi
\(x+3>0\)
\(\Leftrightarrow x>-3\)
g) \(\dfrac{6x-2}{\sqrt{x}-3}\)
Xác định khi:
\(\left\{{}\begin{matrix}\sqrt{x}\ge0\\\sqrt{x}-3\ne0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
h) \(\sqrt{x^2-16}=\sqrt{\left(x+4\right)\left(x-4\right)}\)
Xác định khi
\(\left\{{}\begin{matrix}\left\{{}\begin{matrix}x+4< 0\\x-4< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x+4\ge0\\x-4\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}x< -4\\x< 4\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge-4\\x\ge4\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< -4\\x\ge4\end{matrix}\right.\)
A
2
27 tháng 10 2021
Câu 6
Thay x=-1 và y=2 vào (d), ta được:
-m+1+2m-3=2
\(\Leftrightarrow m=4\)
27 tháng 10 2021
Câu 5:
Gọi đths cần tìm là \(y=ax+b\left(a\ne0\right)\)
Vì đt vuông góc với \(y=2x+7\) nên \(2a=-1\Leftrightarrow a=-\dfrac{1}{2}\)
Do đó hệ số góc của đt là \(a=-\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
Rút gọn được \(A=\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(B-8A\le0\Leftrightarrow\dfrac{x+16}{\sqrt{x}-3}-\dfrac{8\sqrt{x}}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{x-8\sqrt{x}+16}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-4\right)^2}{\sqrt{x}-3}\le0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-4=0\\\sqrt{x}-3< 0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=16\\x< 9\end{matrix}\right.\)
Kết hợp ĐKXD ta được: \(\left[{}\begin{matrix}x=16\\0\le x< 9\end{matrix}\right.\)
14 tháng 5 2023
b: =(m-1)^2-4(-m^2-2)
=m^2+2m+1+4m^2+8
=5m^2+2m+9
=5(m^2+2/5m+9/5)
=5(m^2+2*m*1/5+1/25+44/25)
=5(m+1/5)^2+44/5>=44/5>0 với mọi m
=>PT luôn có hai nghiệm pb
H
3 tháng 6 2023
3.2:
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2+m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1+x_2\right)^2=\left(2m+2\right)^2=4m^2+8m+4\\4x_1x_2=4m^2+4m\end{matrix}\right.\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4m+4=2\left(2m+2\right)=2\left(x_1+x_2\right)\)
\(\Rightarrow\left(x_1+x_2\right)^2-4x_1x_2-2\left(x_1+x_2\right)=4m^2+8m+4-4m^2-4m-4m-4=0\)
Vậy hệ thức liên hệ giữa \(x_1\) và \(x_2\) mà không phụ thuộc vào tham số m là \(\left(x_1+x_2\right)^2-4x_1x_2-2\left(x_1+x_2\right)\)
3 tháng 6 2023
2: x1+x2=2m+2; x1x2=m^2+m
(x1+x2)^2-4x1x2
=4m^2+8m+4-4m^2-4m=4m+4
=>(x1+x2)^2-4x1x2-2(x1+x2)=4m+4-4m-4=0 ko phụ thuộc m
DM
1