
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔCDA vuông tại A và ΔCBA vuông tại A có
CA chug
DA=BA
Do đó:ΔCDA=ΔCBA
b: Ta có: ΔCDB cân tại C
mà CA là đường cao
nên CA là đường phân giác
c: Xét ΔCEI vuông tại E và ΔCFI vuôg tại F có
CI chung
\(\widehat{ECI}=\widehat{FCI}\)
Do đó:ΔCEI=ΔCFI
Suy ra: CE=CF
Xét ΔCDB có CE/CD=CF/CB
nên EF//DB

6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔDAK=ΔDEC
b: ΔDAK=ΔDEC
=>AK=EC
ΔBAD=ΔBED
=>BA=BE
BA+AK=BK
BE+EC=BC
mà BA=BE và AK=EC
nên BK=BC
d:
Xét ΔBKC có BK=BC
nên ΔBKC cân tại B
ΔBKC cân tại B
mà BH là đường phân giác
nên H là trung điểm của CK
=>HK=HC

Câu 15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{a-b+c}{2-3+5}=\dfrac{-10.2}{4}=-2.55\)
Do đó: a=-5,1; b=-7,65; c=-12,75


Tham khảo: (Chúc em học giỏi =)
b)Giá trị (x) 5 7 8 9 10 14
Tần số (n) 4 3 8 8 4 3 N= 30
Nhận xét:
- Có 30 giá trị. Có 6 giá trị khác nhau
- Chỉ có 4 học sinh làm được bài nhanh nhất: 5 phút
- Có đến 3 học sinh làm được bài chậm nhất: 14 phút
- Số phút học sinh làm được bài thuộc vào khoảng : 8-9 phút
c)Tính Trung bình cộng:
_
X = 4.5+7.3+8.8+9.8+10.4+14.3 / 30= 259:30 = 8,6 phút


\(2x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{2}\)
Áp dụng TCDTSBN ta có:
\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{3x+4y}{15+8}=\dfrac{46}{23}=2\)
\(\dfrac{x}{5}=2\Rightarrow x=10\\ \dfrac{y}{2}=2\Rightarrow y=4\)
Theo đề ra ta có: 2x = 5y => \(\dfrac{x}{5} = \dfrac{y}{2}\) và 3x + 4y = 46
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5} = \dfrac{y}{2} = \dfrac{3x +4y}{3 . 5 + 4 . 2} = \dfrac{46}{23} = 2\)
=> x = 2 . 5 = 10
=> y = 2 . 2 = 4
Vậy x = 10, y =4

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
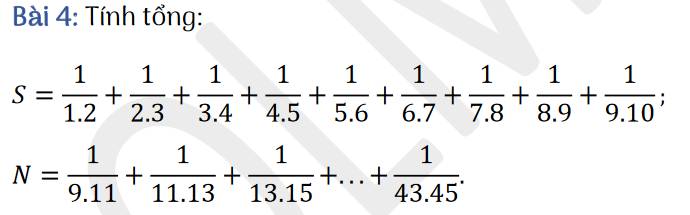

 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
 Giúp em với ăn em cảm ơn mà giúp em mỗi câu 16 thui ạ
Giúp em với ăn em cảm ơn mà giúp em mỗi câu 16 thui ạ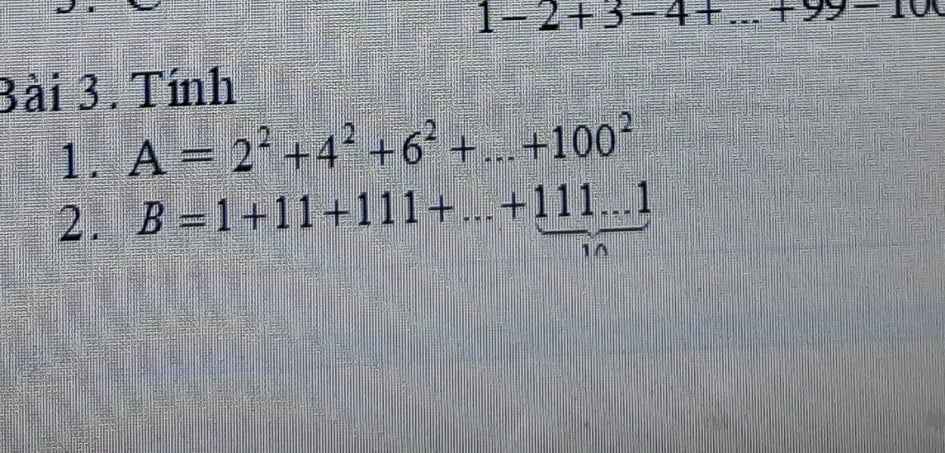 giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn
giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn

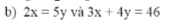


S \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{9.10}\)
\(S=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(S=1-\dfrac{1}{10}\)
\(S=\dfrac{9}{10}\)
N= \(\dfrac{1}{9.11}+\dfrac{1}{11.13}+\dfrac{1}{13.15}+\dfrac{1}{15.16}+...+\dfrac{1}{43.47}\)
N= \(\dfrac{1}{2}.\left(\dfrac{2}{9.11}+\dfrac{2}{11.13}+\dfrac{2}{13.15}+...+\dfrac{2}{43.45}\right)\)
N= \(\dfrac{1}{2}.\left(\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{15}+...+\dfrac{1}{43}-\dfrac{1}{45}\right)\)
N= \(\dfrac{1}{2}.\left(\dfrac{1}{9}-\dfrac{1}{45}\right)\)
N=\(\dfrac{1}{2}\) . \(\dfrac{4}{45}\)
N= \(\dfrac{2}{45}\)