
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5:
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y-z}{2+3-4}=\dfrac{-20}{1}=-20\)
Do đó: x=-40; y=-60; z=-80

Câu 2:
a, Vì m⊥MN và n⊥MN nên m//n
b, Vì m//n nên \(\widehat{D_1}=\widehat{C}=45^0\) (so le trong)
c, Vì m//n nên \(\widehat{D_1}=\widehat{C_1}\) (đồng vị)

a) \(\Rightarrow\left|\dfrac{3}{4}+x\right|=0\Rightarrow\dfrac{3}{4}+x=0\Rightarrow x=-\dfrac{3}{4}\)
b) \(\Rightarrow x+0,4=\dfrac{4}{9}:\dfrac{2}{3}=\dfrac{2}{3}\Rightarrow x=\dfrac{2}{3}-0,4=\dfrac{4}{15}\)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BC=6cm
nên BM=3cm
=>AM=4cm
d: Xét ΔABC cân tại A có AM là đường cao
nên AM là phân giác của góc BAC
Xét ΔABC có
AM là đường phân giác
BI là đường phân giác
AM cắt BI tại I
Do đó: CI là tia phân giác của góc ACB

Gọi số học sinh mỗi loại của khối 7 lần lượt là: \(a,b,c\left(a,b,c>0\right)\)
Áp dụng tc dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{6}=\dfrac{a+b+c}{4+5+6}=\dfrac{120}{15}=8\)
\(=>\left\{{}\begin{matrix}a=32\left(hs\right)\\b=40\left(hs\right)\\c=48\left(hs\right)\end{matrix}\right.\)
Vậy...........


Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5

Câu 2:
a: \(=xy^5\cdot\dfrac{1}{4}x^6\cdot\left(-8\right)y^3z^3=-2x^7y^8z^3\)
b: \(f\left(1\right)=3\cdot1^2-4+1=0\)
=>x=1 là nghiệm của f(x)
\(f\left(-\dfrac{1}{3}\right)=3\cdot\dfrac{1}{9}-4\cdot\dfrac{-1}{3}+1=\dfrac{1}{3}+\dfrac{4}{3}+1=\dfrac{8}{3}\)
=>x=-1/3 không là nghiệm của f(x)
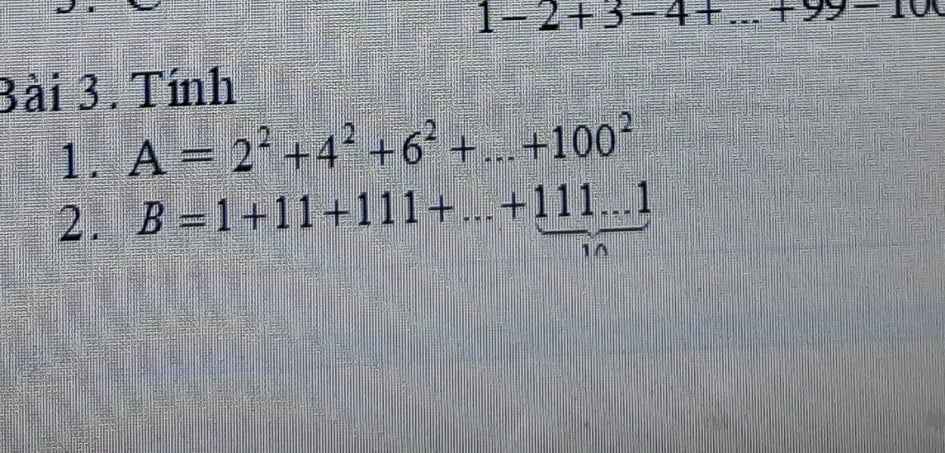 giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn
giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33 
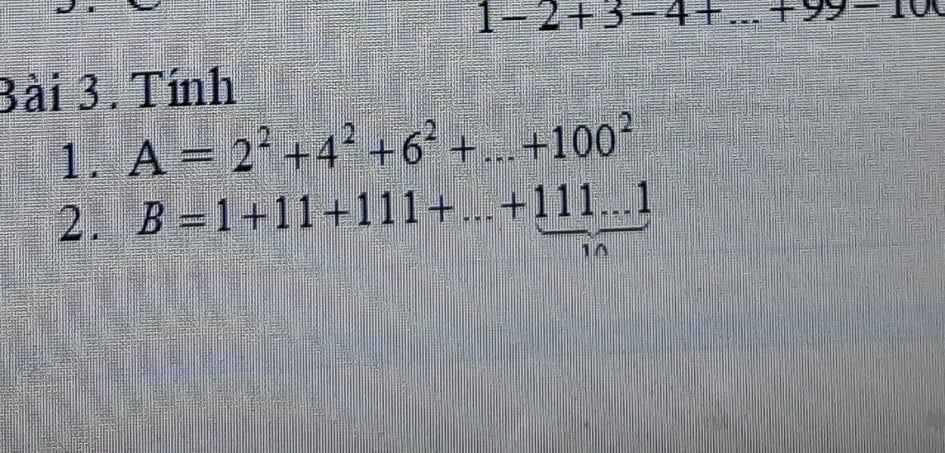 mng giúp em câu a với ạ <33 em cảm ơn
mng giúp em câu a với ạ <33 em cảm ơn
 mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>

 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ