MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LB
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
1
30 tháng 9 2021
Bài 5:
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y-z}{2+3-4}=\dfrac{-20}{1}=-20\)
Do đó: x=-40; y=-60; z=-80
30 tháng 7 2023
2:
a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
=>ΔABD=ΔACD
b: ΔABD=ΔACD
=>góc ADB=góc ADC=180/2=90 độ
=>AD vuông góc BC
c: BC=12
=>BD=CD=6
AD=căn 10^2-6^2=8
d: BN=AB/2
CM=AC/2
mà AB=AC
nên BN=CM
Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>NC=BM
e: Xét ΔABC có
BM,CN là trung tuyến
BM cắt CN tại G
=>G là trọng tâm
=>A,G,D thẳng hàng và AG=2/3AD=16/3
mng giúp em câu a với ạ <33 em cảm ơn
mng giúp em với ạ.Em rất cảm ơn mọi người ạ
6 tháng 4 2022
a: AC=12cm
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔABC vuông tại A và ΔAEC vuông tại A có
AB=AE
AC chung
Do đó: ΔABC=ΔAEC
c: Xét ΔCEB có
CA là đường trung tuyến
BH là đường trung tuyến
CA cắt BH tại M
Do đó: M là trọng tâm của ΔCEB
15 tháng 2 2020
Ta có: \(\frac{x+2}{y+10}\)\(=\)\(\frac{1}{5}\)\(\Rightarrow\)\(5\left(x+2\right)=y+10\)(1)
\(y-3x=2\)\(\Rightarrow\)\(y+2=3x\) (2)
Thay (2) vào (1) ta có:
\(5\left(x+2\right)=\left(y+2\right)+8\)
\(5x+10=3x+8\)
\(5x-3x=8-10\)
\(2x=-2\)
\(x=-2:2\)
\(x=-1\)
Vậy: x=-1
Chúc bạn làm bài tốt!
18 tháng 5 2022
a,
Ta có :
2BD = BC
=> 2BD = 6
=> BD = 3 (cm)
Ta có :
Δ ABC cân tại A
AD là đường trung trực
=> AD là đường cao
=> AD là đường trung tuyến
Xét Δ ADB vuông tại D, có :
\(AB^2=AD^2+BD^2\) (Py - ta - go)
=> \(6^2=AD^2+3^2\)
=> \(27=AD^2\)
=> AD = 5,1 (cm)
18 tháng 5 2022
b,
Xét Δ ABG và Δ ACG, có :
AG là cạnh chung
AB = AC (Δ ABC cân tại A)
\(\widehat{BAG}=\widehat{CAG}\) (AD là tia phân giác \(\widehat{BAC}\))
=> Δ ABG = Δ ACG (c.g.c)
=> \(\widehat{ABG}=\widehat{ACG}\)
c,
Ta có :
G là trọng tâm
Mà AD là đường trung trực
=> A,G,D thẳng hàng
d,
Điều cần chứng minh : BC + 2AD > AB + AC
Ta có :
BC = 6 (cm)
AD = 5,1 (cm)
AB = AC = 5 (cm)
Thế số :
6 + 2. 5,1 > 5 + 5
=> 16,2 > 10
=> BC + 2AD > AB + AC (đpcm)
18 tháng 5 2022
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH và \(\widehat{BAH}=\widehat{CAH}\)
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
d: XétΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE
hay ΔADE cân tạiA
19 tháng 5 2022
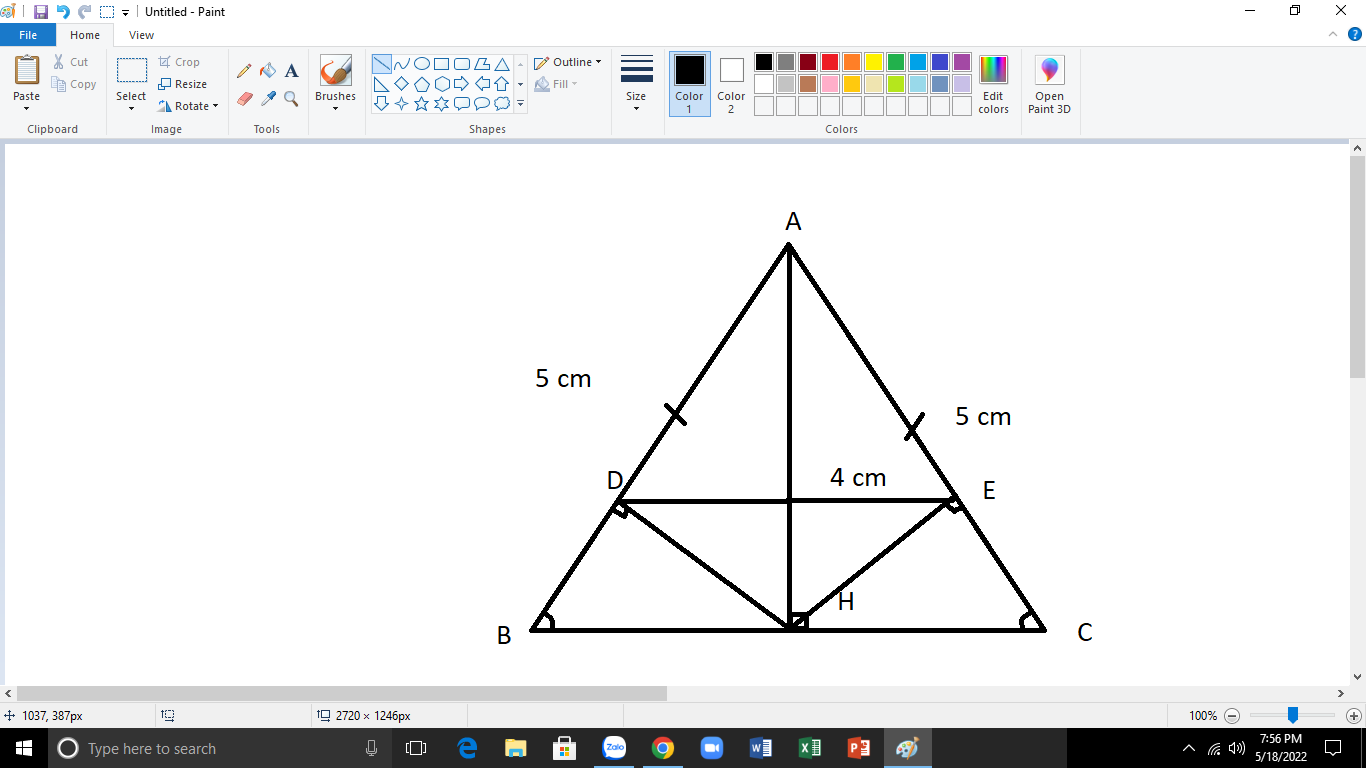
\(\text{a)Xét }\Delta ABH\text{ và }\Delta ACH\text{ có:}\)
\(\left\{{}\begin{matrix}AH\text{ chung}\\AB=AC=5cm\left(gt\right)\\\widehat{B}=\widehat{C}\left(\Delta ABC\text{ cân tại A}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c-g-c\right)\)
\(\Rightarrow BH=CH\left(\text{hai cạnh tương ứng}\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\left(\text{hai góc tương ứng}\right)\)
\(\text{b)Xét }\Delta BAH\text{ vuông tại H có:}\)
\(AB^2=AH^2+BH^2\left(\text{định lí Py ta go}\right)\)
\(\Rightarrow BH^2=AB^2-AH^2\)
\(\Rightarrow BH^2=5^2-4^2=25-16=9\left(cm\right)\)
\(\Rightarrow BH=\sqrt{9}=3\left(cm\right)\)
\(\text{d)Xét }\Delta ADH\text{ và }\Delta AEH\text{ có:}\)
\(\left\{{}\begin{matrix}AH\text{ chung}\\\widehat{ADH}=\widehat{AEH}=90^0\left(gt\right)\\\widehat{DAH}=\widehat{EAH}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ADH=\Delta AEH\left(g-c-g\right)\)
\(\Rightarrow AD=AE\left(\text{hai cạnh tương ứng}\right)\)
\(\Rightarrow\Delta ADE\text{ cân tại A}\)
Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5