
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}< >-\dfrac{1}{m}\)
=>\(m^2\ne-3\)(luôn đúng)
Ta có: \(\left\{{}\begin{matrix}mx-y=2\\3x+my=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\left(mx-2\right)=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m^2x-2m=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=m\cdot\dfrac{5m}{m^2+3}-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=\dfrac{5m^2-2m^2-6}{m^2+3}=\dfrac{3m^2-6}{m^2+3}\end{matrix}\right.\)
\(\left(x+y\right)\cdot\left(m^2+3\right)+8=0\)
=>\(\dfrac{5m+3m^2-6}{m^2+3}\cdot\left(m^2+3\right)+8=0\)
=>\(3m^2+5m-6+8=0\)
=>\(3m^2+5m+2=0\)
=>(m+1)(3m+2)=0
=>\(\left[{}\begin{matrix}m=-1\\m=-\dfrac{2}{3}\end{matrix}\right.\)

1. ĐKXĐ: $x\geq 1$
PT $\Leftrightarrow \sqrt{x-1}=13-x$
\(\Rightarrow \left\{\begin{matrix} 13-x\geq 0\\ x-1=(13-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 13\\ x^2-27x+170=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 13\\ (x-17)(x-10)=0\end{matrix}\right.\)
\(\Rightarrow x=10\) (tm)
2. ĐKXĐ: $x\geq 3$
\(3\sqrt{x+34}-3\sqrt{x-3}=1\)
\(\Leftrightarrow 3\sqrt{x+34}=3\sqrt{x-3}+1\)
\(\Rightarrow 9(x+34)=9x+6\sqrt{x-3}-26\)
\(\Leftrightarrow \frac{166}{3}=\sqrt{x-3}\)
$\Leftrightarrow x-3=\frac{27556}{9}$
$\Leftrightarrow x=\frac{27583}{9}$ (tm)

Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi

II/ Bài tập tham khảo:
Bài 4:
\(A=sin^21^0+sin^22^0+sin^23^0+...+sin^288^0+sin^289^0\)
\(A=\left(sin^21^0+sin^289^0\right)+\left(sin^22^0+sin^288^0\right)+...+\left(sin^244^0+sin^246^0\right)+sin^245^0\)
\(A=\left(sin^21^0+cos^21^0\right)+\left(sin^22^0+cos^22^0\right)+...+\left(sin^244^0+cos^244^0\right)+\left(\frac{\sqrt{2}}{2}\right)^2\)
\(A=1+1+...+1+1\)(45 số hạng tất cả)
(vì \(\sin^2\alpha+\cos^2\alpha=1\)và \(\left(\frac{\sqrt{2}}{2}\right)^2=1\)
A = 45

a) Xét đường tròn (O; 15 cm) có: OM = ON = 15 cm
⇒ O nằm trên đường trung trực của MN
Xét đường tròn (O'; 20 cm) có: O'M = O'N = 20 cm
⇒ O' nằm trên đường trung trực của MN
⇒ OO' là đường trung trực của MN hay OO' ⊥ MN

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

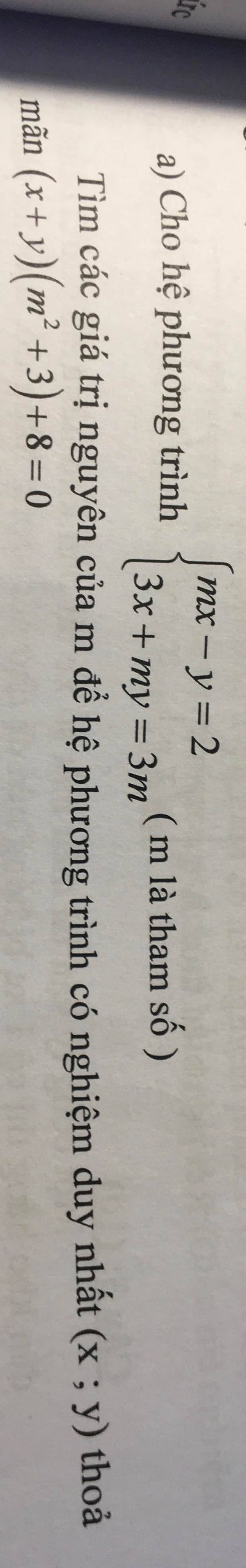




 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
d: \(=\dfrac{-9\sqrt{3}-6\sqrt{2}}{19}-\dfrac{\sqrt{3}}{5}\)
\(=\dfrac{-64\sqrt{3}-30\sqrt{2}}{95}\)
b: \(=\dfrac{37\left(7-2\sqrt{3}\right)}{49-12}=7-2\sqrt{3}\)