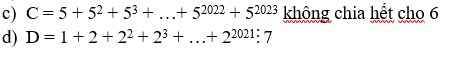Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(-135\right).29-13.135+42.\left(-65\right)\\ =135.\left(-29\right)-13.135+42.\left(-65\right)\\ =135.\left(-29-13\right)+42.\left(-65\right)\\ =135.\left(-42\right)+\left(-42\right).65\\ =\left(-42\right).\left(135+65\right)\\ =\left(-42\right).200\\ =-8400\)
F = (-135). 29 - 13. 135 + 42. (-65).
F = (-135). (29 + 13) + 42. (-65).
F = (-135). 42 - 42. 65.
F = -42. (135 + 65).
F = -42. 200
F = -8400.

\(a,42=2\cdot3\cdot7\\ 98=2\cdot7^2\\ \RightarrowƯCLN\left(42,98\right)=14\\ \RightarrowƯC\left(42,98\right)=Ư\left(14\right)=\left\{1;2;7;14\right\}\\ b,63=3^2\cdot7\\ 105=3\cdot5\cdot7\\ \RightarrowƯCLN\left(63,105\right)=21\\ \RightarrowƯC\left(63,105\right)=Ư\left(21\right)=\left\{1;3;7;21\right\}\)

\(\Leftrightarrow1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{8}{9}\)
\(\Leftrightarrow1-\dfrac{1}{x+1}=\dfrac{8}{9}\)
\(\Leftrightarrow\dfrac{1}{x+1}=\dfrac{1}{9}\)
=>x+1=9
hay x=8
\(\Leftrightarrow\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{8}{9}\)
\(\Leftrightarrow1-\dfrac{1}{x+1}=\dfrac{8}{9}\)
\(\Leftrightarrow-\dfrac{1}{x+1}=\dfrac{8}{9}-1\)
\(\Leftrightarrow-\dfrac{1}{x+1}=-\dfrac{1}{9}\)
\(\Leftrightarrow x+1=9\)
\(\Leftrightarrow x=8\)


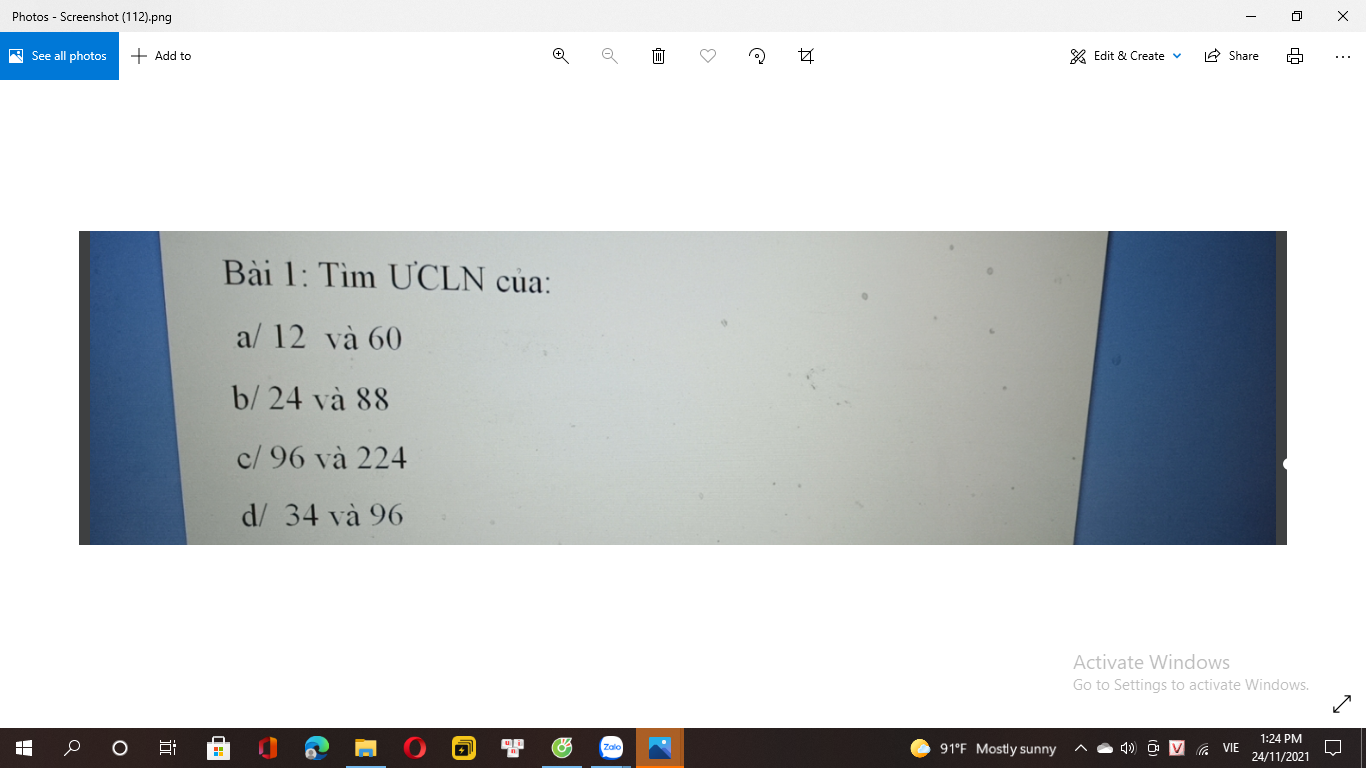
a) \(12=2^2.3\) \(60=2^2.3.5\)
\(ƯCLN\left(12;60\right)=2^2=4\)
b) \(24=2^2.3.2\)
12 = 22 x 3
60 = 22 x 3 x 5
ƯCLN (12, 60) = 22 . 3 = 12
24 = 23 x 3
88 = 23 x 11
ƯCLN (24, 88) = 23 = 8
96 = 25 x 3
224 = 25 x 7
ƯCLN (96, 224) = 25 = 32
34 = 2 x 17
96 = 25 x 3
ƯCLN (34, 96) = 2

Lời giải:
a. Gọi 3 số tự nhiên liên tiếp là $a, a+1, a+2$. Tổng của 3 số là:
$a+(a+1)+(a+2)=3a+3=3(a+1)\vdots 3$
Ta có đpcm.
b.
Gọi 2 số chẵn liên tiếp là $2k+2$ và $2k+4$ với $k$ là số tự nhiên.
Tổng 2 số chẵn liên tiếp là:
$2k+2+2k+4=4k+6=4(k+1)+2$ chia 4 dư 2 (tức là không chia hết cho 4)
Do đó ta có đpcm.
c.
Trong 2 số tự nhiên liên tiếp luôn tồn tại 1 số chẵn và 1 số lẻ. Do đó tích của chúng sẽ luôn là số chẵn (chia hết cho 2), vì chẵn x lẻ = chẵn.
d. Gọi 3 số tự nhiên liên tiếp là $a, a+1, a+2$
Nếu $a$ chia hết cho 3 thì $a(a+1)(a+2)\vdots 3$
Nếu $a$ chia 3 dư 1 thì $a+2\vdots 3\Rightarrow a(a+1)(a+2)\vdots 3$
Nếu $a$ chia 3 dư 2 thì $a+1\vdots 3\Rightarrow a(a+1)(a+2)\vdots 3$
Vậy $a(a+1)(a+2)$ luôn chia hết cho 3 trong mọi trường hợp
Do đó ta có đpcm.

1/
$C=5+(5^2+5^3)+(5^4+5^5)+.....+(5^{2022}+5^{2023})$
$=5+5^2(1+5)+5^4(1+5)+....+5^{2022}(1+5)$
$=5+(1+5)(5^2+5^4+....+5^{2022})$
$=5+6(5^2+5^4+....+5^{2022})$
$\Rightarrow C$ chia $6$ dư $5$
$\Rightarrow C\not\vdots 6$
2/
$D=(1+2+2^2)+(2^3+2^4+2^5)+....+(2^{2019}+2^{2020}+2^{2021})$
$=(1+2+2^2)+2^3(1+2+2^2)+....+2^{2019}(1+2+2^2)$
$=(1+2+2^2)(1+2^3+...+2^{2019})$
$=7(1+2^3+...+2^{2019})\vdots 7$
Ta có đpcm.



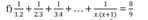 giúp em với ạ,em cần gấp!!!!!!!
giúp em với ạ,em cần gấp!!!!!!!