K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 12 2022
\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}=\dfrac{2\sqrt{a}}{\sqrt{a}}=2\)
6 tháng 1 2022
a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do dó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do dó: ΔBEC vuông tại E
Xét ΔABC có
BE là đường cao
CD là đường cao
BE cắt CD tại H
Do đó: AH⊥BC
b: Xét tứ giác ADHE có
\(\widehat{ADH}+\widehat{AEH}=180^0\)
Do đó: ADHE là tứ giác nội tiếp
NH
1
31 tháng 8 2021
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
30 tháng 11 2021
\(1,=10\sqrt{2}-21\sqrt{2}+3\sqrt{2}=-8\sqrt{2}\\ 2,=\dfrac{6\left(\sqrt{5}+1\right)}{4}=\dfrac{3\sqrt{5}+3}{2}\\ 3,=2+\left|2-\sqrt{7}\right|=2+\sqrt{7}-2=\sqrt{7}\)
12 tháng 8 2021
Bạn mua những cuốn sách tham khảo ở nhà sách đi bạn
CS
28 tháng 10 2021
\(\sqrt{x^2-16}-2\sqrt{x-4}=0\left(đk:x\ge4\right)\)
\(\Leftrightarrow\sqrt{\left(x-4\right)\left(x+4\right)}-2\sqrt{x-4}=0\)
\(\Leftrightarrow\sqrt{x-4}\left(\sqrt{x+4}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-4}=0\\\sqrt{x+4}=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+4=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\)
NM
2
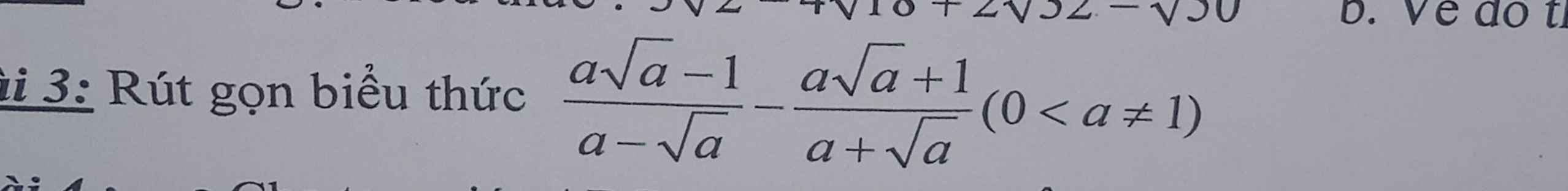
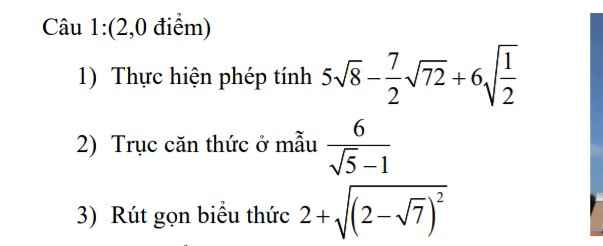
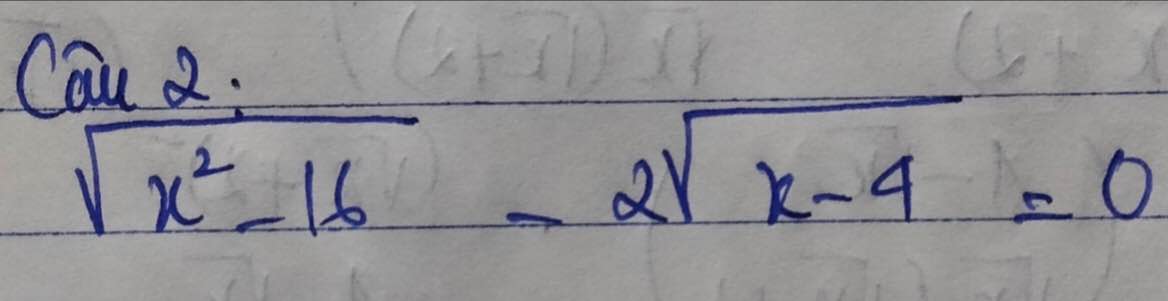
`D=(a+4sqrta+4)/(sqrta+2)+(4-a)/(sqrta-2)`
`=(sqrta+2)^2/(sqrta+2)+((2-sqrta)(2+sqrta))/(sqrta-2)`
`=sqrta+2-(2+sqrta)`
`=0`
ĐK: a ≥ 0; a khác 4
\(D=\dfrac{a+\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}\)
\(=\dfrac{a+\sqrt{a}+4}{\sqrt{a}+2}-\left(2+\sqrt{a}\right)\)
\(=\dfrac{\left(a+\sqrt{a}+4\right)-\left(2+\sqrt{a}\right)^2}{\sqrt{a}+2}=\dfrac{a+\sqrt{a}+4-\left(4+4\sqrt{a}+a\right)}{\sqrt{a}+2}=\dfrac{a+\sqrt{a}+4-4-4\sqrt{a}-a}{\sqrt{a}+2}=-\dfrac{3}{\sqrt{a}}\)