
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2

Bài 9:
a: Xét tứ giác OPMN có
góc OPM+góc ONM=180 độ
=>OPMN là tứ giác nội tiếp
b: \(MN=\sqrt{10^2-6^2}=8\left(cm\right)\)
c: ΔOAB cân tại O
mà OH là đường trung tuyến
nên OH vuông góc AB
Xét tứ giác OHNM có
góc OHM=goc ONM=90 độ
=>OHNM là tứ giác nội tiép
=>góc MHN=góc MON

a:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc CMO+góc CIO=180 độ
=>CIOM nội tiếp

a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
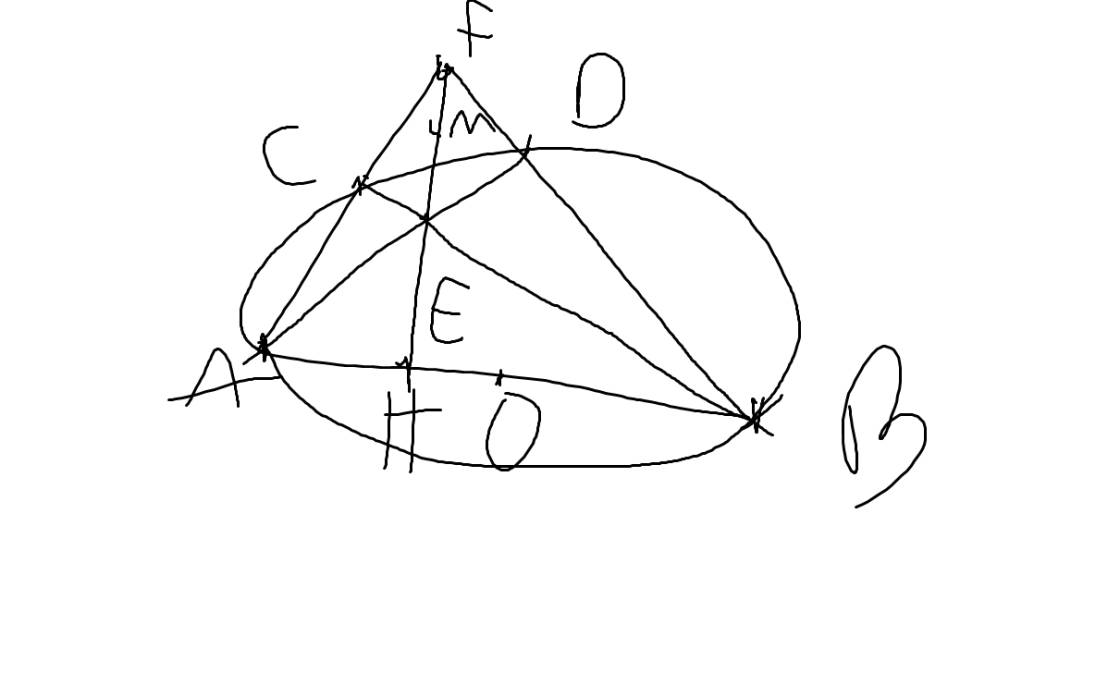

a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp đường tròn đường kính AB
=>I là trung điểm của AB
b: Gọi H là giao của AD và BE
ABDE nội tiếp
=>góc HDE=góc HBA
=>góc HDE=góc HMN
=>DE//MN

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

`D=(a+4sqrta+4)/(sqrta+2)+(4-a)/(sqrta-2)`
`=(sqrta+2)^2/(sqrta+2)+((2-sqrta)(2+sqrta))/(sqrta-2)`
`=sqrta+2-(2+sqrta)`
`=0`
ĐK: a ≥ 0; a khác 4
\(D=\dfrac{a+\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}\)
\(=\dfrac{a+\sqrt{a}+4}{\sqrt{a}+2}-\left(2+\sqrt{a}\right)\)
\(=\dfrac{\left(a+\sqrt{a}+4\right)-\left(2+\sqrt{a}\right)^2}{\sqrt{a}+2}=\dfrac{a+\sqrt{a}+4-\left(4+4\sqrt{a}+a\right)}{\sqrt{a}+2}=\dfrac{a+\sqrt{a}+4-4-4\sqrt{a}-a}{\sqrt{a}+2}=-\dfrac{3}{\sqrt{a}}\)


 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ









a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do dó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do dó: ΔBEC vuông tại E
Xét ΔABC có
BE là đường cao
CD là đường cao
BE cắt CD tại H
Do đó: AH⊥BC
b: Xét tứ giác ADHE có
\(\widehat{ADH}+\widehat{AEH}=180^0\)
Do đó: ADHE là tứ giác nội tiếp