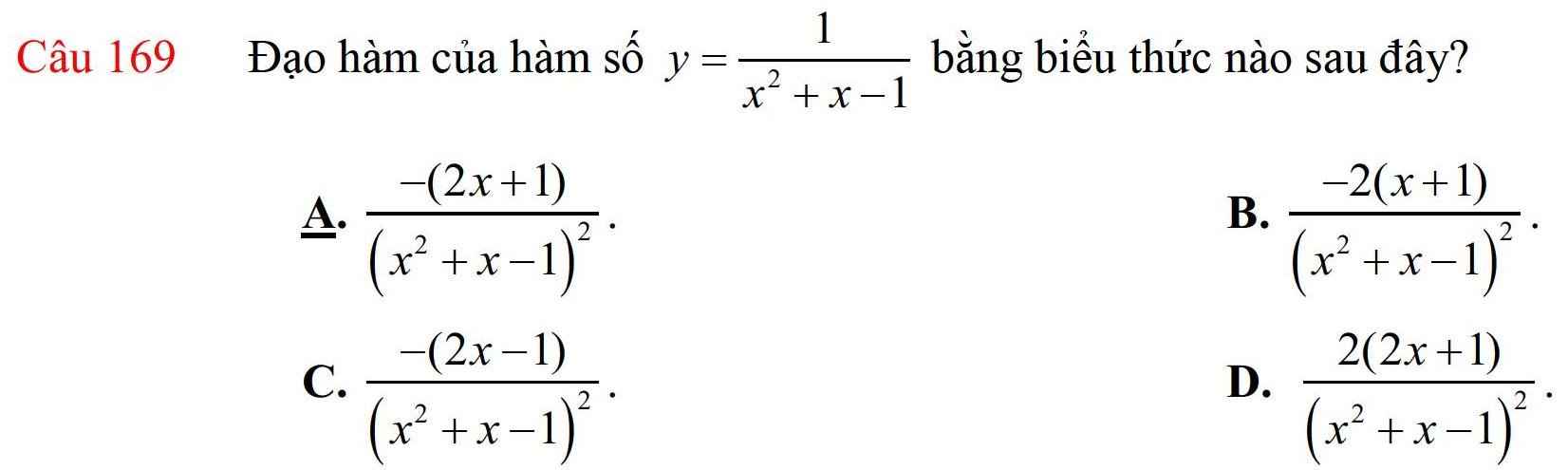K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 10 2021
Chọn 4 cuốn sách bất kì: \(C_{12}^4=495\) cách
Chọn 4 cuốn sách sao cho có đủ 3 môn:
\(C_5^1.C_4^1.C_3^1=60\) cách
Chọn 4 cuốn sao cho không thuộc quá 2 môn:
\(495-60=435\) cách
HP
6 tháng 9 2021
1.
ĐK: \(\left\{{}\begin{matrix}\dfrac{1+sinx}{1-sinx}\ge0\\1-sinx\ne0\end{matrix}\right.\Leftrightarrow1-sinx\ne0\Leftrightarrow sinx\ne1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
TT
1
DT
7 tháng 3 2022
Áp dụng công thức \(\left(\dfrac{1}{v}\right)'=\dfrac{-v'}{v^2}\)
Ta có \(y'=\dfrac{-\left(x^2+x-1\right)'}{\left(x^2+x-1\right)^2}=-\dfrac{\left(2x+1\right)}{\left(x^2+x-1\right)^2}\)
TG
4
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
2.
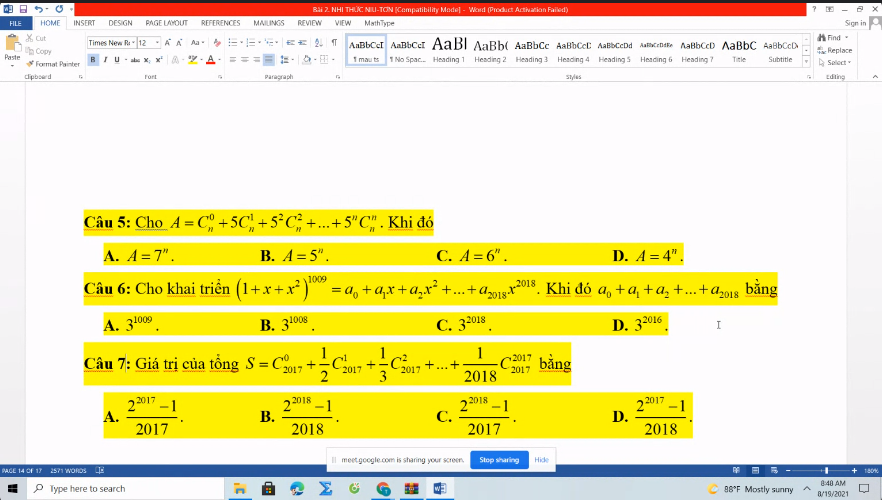
Xét khai triển:
\(\left(1+x\right)^{2017}=C_{2017}^0+C_{2017}^1.x+C_{2017}^2x^2+...+C_{2017}^{2017}x^{2017}\)
Cho \(x=1\) ta được:
\(2^{2017}=C_{2017}^0+C_{2017}^1+...+C_{2017}^{2017}\)
\(\Rightarrow C_{2017}^1+C_{2017}^2+...+C_{2017}^{2017}=2^{2017}-C_{2017}^0=2^{2017}-1\)
3.
Xét khai triển:
\(\left(1+x\right)^{10}=C_{10}^0+C_{10}^1x+...+C_{10}^{10}x^{10}\)
Thay \(x=2\) ta được:
\(3^{10}=C_{10}^0+2C_{10}^1+2^2C_{10}^2+...+2^{10}C_{10}^{10}\)
\(\Rightarrow S=3^{10}\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
4.
Xét khai triển:
\(\left(1+x\right)^{15}=C_{15}^0+C_{15}^1x+...+C_{15}^{15}x^{15}\)
Thay \(x=1\) ta được:
\(2^{15}=C_{15}^0+C_{15}^1+...+C_{15}^{15}\)
Mặt khác, áp dụng công thức: \(C_n^k=C_n^{n-k}\) ta có:
\(C_{15}^0=C_{15}^{15}\)
\(C_{15}^1=C_{15}^{14}\)
...
\(C_{15}^7=C_{15}^8\)
Cộng vế:
\(C_{15}^0+C_{15}^1+...+C_{15}^7=C_{15}^8+C_{15}^9+...+C_{15}^{15}\)
\(\Rightarrow C_{15}^0+C_{15}^1+...+C_{15}^{15}=2\left(C_{15}^8+C_{15}^9+...+C_{15}^{15}\right)\)
\(\Rightarrow2S=2^{15}\)
\(\Rightarrow S=2^{14}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 6 2021
Mình bận 1 xíu, nhưng nếu học giới hạn thì bạn cần nắm rõ các khái niệm và các dạng vô định cũng như không phải vô định đã
Giới hạn này không phải là 1 giới hạn vô định (mẫu số xác định và hữu hạn), khi gặp giới hạn kiểu này thì chỉ có 1 cách: thay số tính trực tiếp như lớp 1 là được:
\(\lim\limits_{x\rightarrow\dfrac{\pi}{2}}\dfrac{sin\left(x-\dfrac{\pi}{4}\right)}{x}=\dfrac{sin\left(\dfrac{\pi}{2}-\dfrac{\pi}{4}\right)}{\dfrac{\pi}{2}}=\dfrac{\sqrt{2}}{\pi}\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
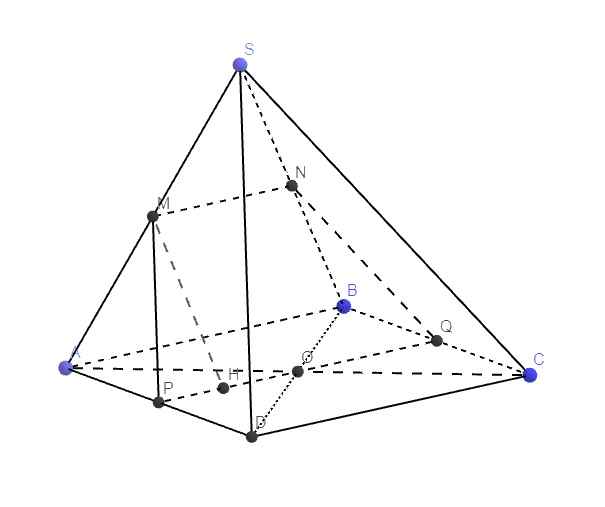
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
PN
0
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 9 2021
6. Trên \(\left[0;\dfrac{\pi}{2}\right]\) hàm \(y=cosx\) giảm còn \(y=sinx\) tăng
\(\Rightarrow\dfrac{1+cosx}{1+sinx}\) giảm
\(\Rightarrow y_{max}=y\left(0\right)=2\)
\(y_{min}=y\left(\dfrac{\pi}{2}\right)=\dfrac{1}{2}\)
7. Hàm không tồn tại GTLN trên khoảng đã cho (x càng gần \(-\dfrac{\pi}{4}\) thì y càng gần dương vô cực)
\(1+tanx\) tăng, không âm \(\Rightarrow\dfrac{1}{1+tanx}\) giảm \(\Rightarrow y_{min}=y\left(\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
