K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 10 2021
a: Thay x=2 và y=3 vào hàm số, ta được:
\(2k+2-4=3\)
\(\Leftrightarrow k=\dfrac{5}{2}\)
NH
1
30 tháng 4 2023
1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t
NH
2
6 tháng 3 2023
1: vecto AC=(-2;2)
=>VTCP là (-2;2); vtpt là (2;2)
2: vecto AB=(-10;-2)=(5;1)
=>VTPT của Δ là (5;1)
vtcp của Δ là (-1;5)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
\(\overrightarrow{AC}=\left(-2;2\right)=2\left(-1;1\right)\) nên đường thẳng AC nhận \(\left(-1;1\right)\) là 1 vtcp và \(\left(1;1\right)\) là 1 vtpt
b.
\(\overrightarrow{BA}=\left(10;2\right)=2\left(5;1\right)\) ; mà \(\Delta\perp AB\) nên \(\Delta\) nhận (5;1) là 1 vtpt và \(\left(1;-5\right)\) là 1 vtcp
24 tháng 10 2021
Phương trình hoành độ giao điểm là:
\(-2x^2+3x+1=mx-2m+1\)
\(\Leftrightarrow-2x^2+\left(3-m\right)x+2m=0\)
Để (P) tiếp xúc với (d) thì \(\left(3-m\right)^2-4\cdot\left(-2\right)\cdot2m=0\)
\(\Leftrightarrow m^2-6m+9+16m=0\)
\(\Leftrightarrow m^2-25m+9=0\)(1)
\(\text{Δ}=\left(-25\right)^2-4\cdot9=625-36=589\)
Vì Δ>0 nên phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{25-\sqrt{589}}{2}\\m_2=\dfrac{25+\sqrt{589}}{2}\end{matrix}\right.\)
BC
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1 2022
Do ABCD là hình thoi \(\Rightarrow\overrightarrow{AD}=\overrightarrow{BC}\), do M là trung điểm AB \(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\)
Do đó:
\(\overrightarrow{MA}+\overrightarrow{MD}+2\overrightarrow{MC}=\overrightarrow{MA}+\left(\overrightarrow{MA}+\overrightarrow{AD}\right)+2\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(=2\left(\overrightarrow{MA}+\overrightarrow{MB}\right)+\overrightarrow{AD}+2\overrightarrow{BC}=\overrightarrow{BC}+2\overrightarrow{BC}=3\overrightarrow{BC}\)
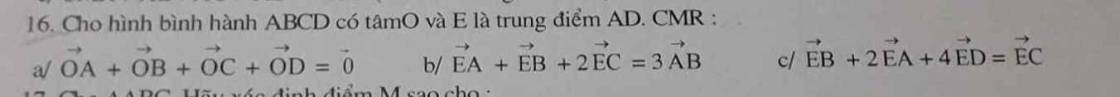
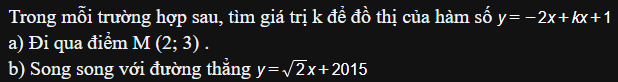
giúp em mấy câu này với ạ
`a)` Vì `O` là trung điểm của `AC;BD`
`=>{(\vec{OA}=-\vec{OC}),(\vec{OB}=-\vec{OD}):}`
Ta có: `\vec{OA}+\vec{OB}+\vec{OC}+\vec{OD}`
`=-\vec{OC}-\vec{OD}+\vec{OC}+\vec{OD}=0`
`b)` Vì `E` là trung điểm `AD=>\vec{EA}=-\vec{ED}`
Ta có: `\vec{EA}+\vec{EB}+2\vec{EC}`
`=\vec{EA}+\vec{EA}+\vec{AB}+2\vec{ED}+2\vec{DC}`
`=-2\vec{ED}+\vec{AB}+2\vec{ED}+2\vec{AB}=3\vec{AB}`
`c)` Ta có: `\vec{EB}+2\vec{EA}+4\vec{ED}`
`=\vec{EB}-2\vec{ED}+4\vec{ED}`
`=\vec{EB}+2\vec{ED}`
`=\vec{EA}+\vec{AB}+2\vec{ED}`
`=-\vec{ED}+\vec{AB}+2\vec{ED}`
`=\vec{AB}+\vec{EC}+\vec{CD}` (Mà `\vec{AB}=-\vec{CD}`)
`=\vec{EC}`