K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PP
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 7 2023
a, \(x^2\) = \(x^3\)
\(x^3\) - \(x^2\) = 0
\(x^2\)( \(x\) -1) = 0
\(\left[{}\begin{matrix}x^2=0\\x-1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(x\) \(\in\) { 0; 1}
e, 32\(x+1\) = 27
\(3^{2x}\)+1 = 33
2\(x\) + 1 = 3
2\(x\) = 2
\(x\) = 1
g, 62 = 6\(x-3\)
2 = \(x-3\)
\(x\) = 3 + 2
\(x\) = 5
H
19 tháng 7 2023
\(a,x^2=x^3\\ \Rightarrow x^2-x^3=0\\ \Rightarrow x^2\left(1-x\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=0\\1-x=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(b,3^{2x+1}=27\\ \Rightarrow3^{2x+1}=3^3\\ \Rightarrow2x+1=3\\ \Rightarrow2x=3-1\\ \Rightarrow2x=2\\ \Rightarrow x=2:2\\ \Rightarrow x=1\)
\(c,6^2=6^{x-3}\\ \Rightarrow6^{x-3}=6^2\\ \Rightarrow x-3=2\\ \Rightarrow x=2+3\\ \Rightarrow x=5\)
22 tháng 6 2016
a) 998.34=(1000−2).34=34000−68=33932
b,\(1990.1990-\left(1990+2\right).1988=1990.1990-1990.1988-2.1988=1990\left(1990-1988\right)-2.1988=1990.2-2.1998=2\left(1990-1998\right)=2.2\)= 4
c. \(\text{(1374.57+678.86).(26.13+74.14)}\)
Câu này đề hơi lạ
9 tháng 5 2019
\(E\subset N\)
\(N=\left\{a;b\right\}=\left\{3;4\right\};\left\{3;5\right\};\left\{4;5\right\}\)
VN
Võ Ngọc Phương
VIP
5 tháng 9 2023
1.
a) \(2^x=128\)
\(2^x=2^7\)
\(=>x=7\)
b) \(8^{x-1}=64\)
\(8^{x-1}=8^2\)
\(=>x-1=2\)
\(x=2+1\)
\(=>x=3\)
c) \(3+3^x=30\)
\(3^x=30-3\)
\(3^x=27=3^3\)
\(=>x=3\)
d) \(\left(x+2\right)=64\) -> đề có thiếu không vậy?
e) \(3^2.x=3^5\)
\(x=3^5:3^2\)
\(=>x=3^3=27\)
f) \(\left(2x-1\right)^3=343\)
\(\left(2x-1\right)^3=7^3\)
\(=>2x-1=7\)
\(2x=7+1\)
\(2x=8\)
\(x=8:2\)
\(=>x=4\)
\(#Wendy.Dang\)
5 tháng 9 2023
a,\(2^x\)=128 b,\(8^{x-1}\)=64 c,3+\(3^x\)=30 d,x+2=64
\(2^7\)=128 \(8^{x-1}\)=\(8^2\) \(3^x\)=30-3 x=64-2
=>x=7 =>x-1=2 \(3^x\)=27 x=62
x=2+1=3 \(3^x\)=\(3^3\)
=>x=3
e,\(3^2\).x=\(3^5\) f,(2x-\(1^3\))=343
x=\(3^5\):\(3^2\) 2x=1+343
x=27 2x=344
x=344:2
x=172
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 11 2023
Ư(4)= {-4;-2;-1;1;2;4}
Ư(-3)= {-3;-1;1;3}
Ư(12)={-12;-6;-4;-3;-2;-1;1;2;3;4;6;12}
Ư(-8)={-8;-4;-2;-1;1;2;4;8}
Ư(-6)={-6;-3;-2;-1;1;2;3;6}
Ư(-20)={-20;-10;-5;-4;-2;-1;1;2;4;5;10;20}
Ư(-10)={-10;-5;-2;-1;1;2;5;10}
Ư(-16)={-16;-8;-4;-2;-1;1;2;4;8;16}
MS
1
15 tháng 10 2021
\(D=8+8^3+8^5+...+8^{2x+1}\)
\(\Rightarrow64D=8^3+8^5+...+8^{2x+3}\)
\(\Rightarrow63D=64D-D=8^3+8^5+...+8^{2x+3}-8-8^3-...-8^{2x+1}=8^{2x+3}-8\)
\(\Rightarrow8^{2x+3}-8+8=8^{51}\)
\(\Rightarrow8^{2x+3}=8^{51}\Rightarrow2x+3=51\Rightarrow2x=48\Rightarrow x=24\)
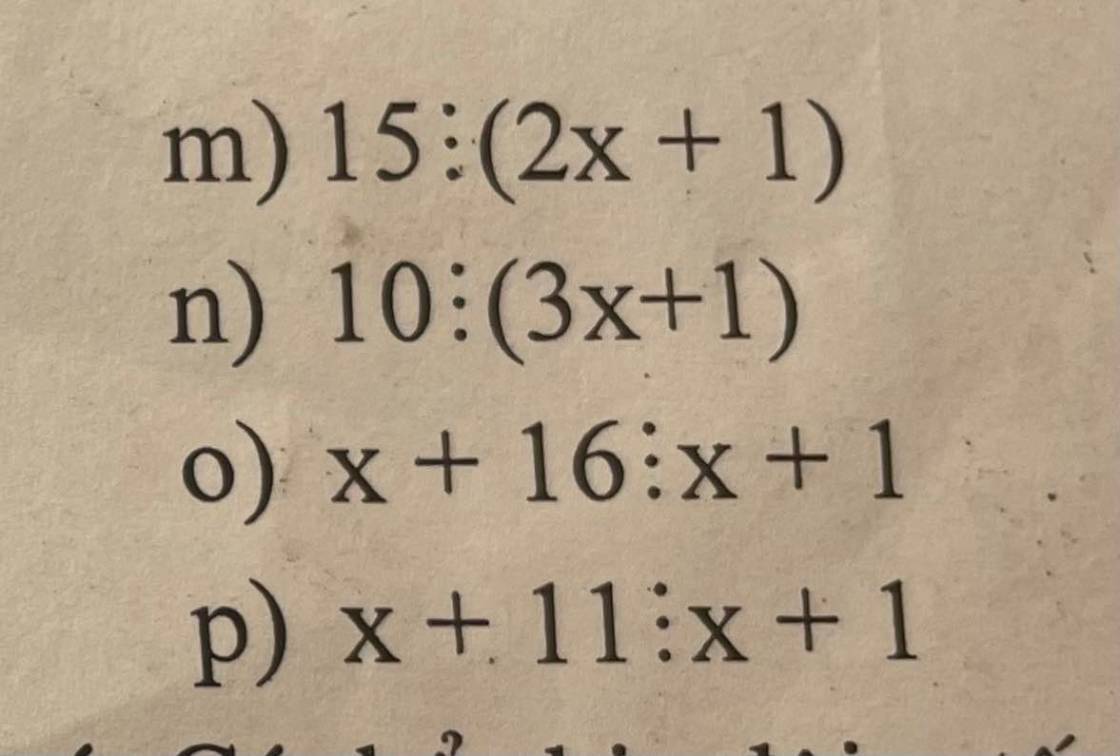
15⋮(2x+1)
=> 2x+1 ϵ Ư(15)
=> 2x+1 ϵ {1;3;5;15}
=> 2x ϵ {0;2;4;14}
=> x ϵ {0;1;2;7}
Vậy x ϵ {0;1;2;7}