
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 20:
Ta có: \(\widehat{A}-\widehat{B}=40^0\Rightarrow\widehat{B}=\widehat{A}-40^0\)
\(\widehat{A}=2\widehat{C}\Rightarrow\widehat{C}=\frac{\widehat{A}}{2}\)
Vì AB//CD (gt) \(\Rightarrow\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)\(\Rightarrow\widehat{D}=180^0-\widehat{A}\)
Tứ giác ABCD \(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\Rightarrow\widehat{A}+\left(\widehat{A}-40^0\right)+\frac{\widehat{A}}{2}+\left(180^0-\widehat{A}\right)=360^0\)
Và đến đây bạn dễ dàng tìm được góc A và từ đó suy ra được góc D.
Câu 29: Ta có:
\(\hept{\begin{cases}xy+x+y=3\\yz+y+z=8\\xz+x+z=15\end{cases}}\Leftrightarrow\hept{\begin{cases}xy+x+y+1=4\\yz+y+z+1=9\\xz+x+z+1=16\end{cases}\Leftrightarrow}\hept{\begin{cases}x\left(y+1\right)+\left(y+1\right)=4\\y\left(z+1\right)+\left(z+1\right)=9\\x\left(z+1\right)+\left(z+1\right)=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=4\\\left(y+1\right)\left(z+1\right)=9\\\left(z+1\right)\left(x+1\right)=16\end{cases}}\)
Đặt \(\hept{\begin{cases}x+1=a\\y+1=b\\z+1=c\end{cases}}\)với a,b,c > 1, khi đó ta có
\(\hept{\begin{cases}ab=4\\bc=9\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}abbc=4.9\\c=\frac{9}{b}\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}16b^2=36\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b^2=\frac{36}{16}=\frac{9}{4}\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{3}{2}\\c=\frac{9}{\frac{3}{2}}=6\\a=\frac{16}{6}=\frac{8}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=a-1=\frac{8}{3}-1=\frac{5}{3}\\y=b-1=\frac{3}{2}-1=\frac{1}{2}\\z=c-1=6-1=5\end{cases}}\)
Vậy \(P=x+y+z=\frac{5}{3}+\frac{1}{2}+5=\frac{10+3+30}{6}=\frac{43}{6}\)

Trong hình thang ABCD có: AE=ED(...)
BF=FC(...)
suy ra EF là đường trung bình của hình thang ABCD
suy ra EF//AB//DC suy ra EF//CD (1)
Trong tam giác ADC có: AE=ED(..)
AM=MC(...)
suy ra EM là đường trung bình của tam giác ADC
suy ra EM//CD (2)
Trong tam giác BDC co BN=ND(...)
BF=FC(...)
suy ra FN là đường trung bình của tam giác BDC
suy ra NF//CD(3)
Từ (1);(2) và (3) suy ra
E;N;M;E thẳng hàng
Vì EM là đường trung bình của tam giác ADC (cmt) nên \(EM=\frac{1}{2}CD\)
Trong tam giác ABD có: AE=DE(...)
DN=BN(....)
do đó EN là đường trung bình của tam giác ABD
\(\Rightarrow EN=\frac{1}{2}AB\)
Ta có NE+MN=EM
\(\Rightarrow MN=EM-NE=\frac{1}{2}CD-\frac{1}{2}AB=\frac{1}{2}\left(CD-AB\right)\)

\(9x^2-x+\dfrac{1}{36}\)
\(=\left(3x\right)^2-2\cdot3x\cdot\dfrac{1}{6}+\left(\dfrac{1}{6}\right)^2\)
\(=\left(3x-\dfrac{1}{6}\right)^2\)

\(\dfrac{a^2-64}{3a-9}.\dfrac{3-a}{8-a}\)
\(=\dfrac{a^2-8^2}{3\left(a-3\right)}.\dfrac{a-3}{a-8}\)
\(=\dfrac{\left(a+8\right)\left(a-8\right)}{3\left(a-3\right)}.\dfrac{a-3}{a-8}\)
\(=\dfrac{\left(a+8\right)\left(a-8\right)\left(a-3\right)}{3\left(a-3\right)\left(a-8\right)}\)
\(=\dfrac{a+8}{3}\)

Bài 4:
a) Xét tứ giác DMEC có
ME//DC(gt)
MD//EC(gt)
Do đó: DMEC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Ta có: CDME là hình bình hành(cmt)
nên Hai đường chéo CM và DE cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của DE(gt)
nên I là trung điểm của CM
hay C,M,I thẳng hàng

Vì ABCD là hình chữ nhật ( gt )
⇒ ∠DAB = ∠ABC = ∠BCD = ∠CDA = \(90^o\)
Vì AH ⊥ BD ( gt )
⇒ ∠AHD = ∠AHB = \(90^o\)
Xét △ADH và △BDA, có
∠AHD = ∠BAD ( = \(90^o\) )
∠ADB chung
⇒ △ADH ∼ △BDA (g-g)
b) Xét △AHB vuông tại H, có :
∠HAB + ∠ABH = \(90^o\) (Tính chất tam giác vuông)
Mà ∠DAH + ∠HAB = \(90^o\)
⇒ ∠DAH = ∠ABH
Xét △ADH và △BAH, có :
∠DAH = ∠ABH (cmt)
∠AHD = ∠AHB (=\(90^o\))
⇒ △ADH ∼ △BAH (g-g)
⇒ \(\dfrac{AH}{BH}=\dfrac{DH}{AH}\left(TSĐD\right)\)
⇒ \(AH^2=BH.DH\)
c) \(AH^2=DH.BH\left(cmt\right)\)
⇒ \(AH^2=144\)
⇒ AH = 12cm
Xét △ADH vuông tại D, có :
\(AH^2+DH^2=AD^2\) (Định lí Py - ta - go)
\(12^2+9^2=AD^2\)
⇒ \(AD^2=225\)
⇒ AD = 15cm
Vì △ADH ∼ △BAH (cmt)
⇒ \(\dfrac{AD}{AB}=\dfrac{AH}{BH}\)
⇒ \(AB=\dfrac{AD.BH}{AH}\)
⇒ AB = 20cm
d) Xét △AHB, có :
K là trung điểm của AH ( gt )
M là trung điểm của BH ( gt )
⇒KM là đường trung bình của △AHB
⇒KM // AB
\(KM=\dfrac{1}{2}AB\)
Vì ABCD là hình chữ nhật ( gt )
⇒ AB // CD
AB = CD
Có KM // AB (cmt)
AB // CD (cmt)
⇒ KM // CD
Vì N là trung điểm của DC ( gt )
⇒ DN = NC =\(\dfrac{1}{2}CD\)
\(KM=\dfrac{1}{2}AB\) (cmt)
AB = CD (cmt)
⇒ KM = DN = NC
Xét tứ giác KMND, có :
KM = DN (CMT)
KM // DN (CMT)
⇒ KMND là hình bình hành
Vì ABCD là hình chữ nhật ( gt )
⇒ AB ⊥ AD
Mà : KM // AB (cmt)
⇒ KM ⊥ AD
Gọi Q là giao điểm của KM với AD
⇒ QM là đường cao của △AMD
Xét △AMD, có :
QM là đường cao của △AMD (cmt)
AH là đường cao của △AMD (AH⊥BC)
AH cắt QM tại K
⇒ KD là đường cao của △AMD
⇒ KD ⊥ AM
Vì KMND là hình bình hành (cmt)
⇒ KD // MN
KD ⊥ AM (CMT)
⇒ MN ⊥ AM
⇒ ∠AMN = \(90^o\)



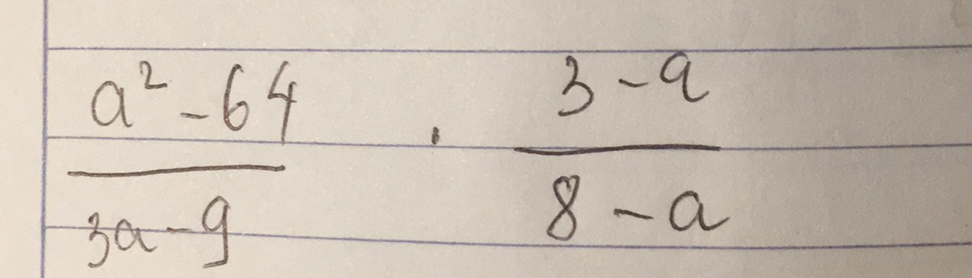
 giúp e bài 4,5 với
giúp e bài 4,5 với
