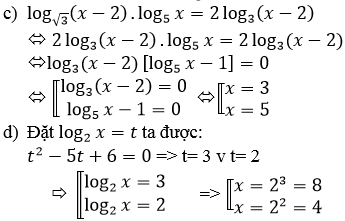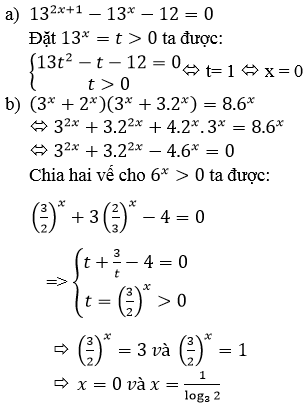NH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
2
DD
15 tháng 4 2016
-log22 x2_ log2x2- 20=0
↔ pt này vô ng bạn ơi!!! xem lại đầu bài.
18 tháng 4 2016
Bài này phương trình có tận 4 nghiệm chứ không phải vô nghiệm đâu bạn Đỗ đại học nhé
Điều kiện \(x\ne0\)
Ta có từ phương trình ban đầu cho \(\Leftrightarrow4\log_2^2\left|x\right|-2\log_2\left|x\right|-20=0\)
\(\Leftrightarrow2\log_2^2\left|x\right|-\log_2\left|x\right|-10=0\)
Đặt \(t=\log_2\left|x\right|\) ta được phương trình \(2t^2-t-10=0\Leftrightarrow\begin{cases}t=-2\\t=\frac{5}{2}\end{cases}\)
Với \(t=2\Rightarrow\log_2\left|x\right|=-2\Leftrightarrow\left|x\right|=\frac{1}{4}\Leftrightarrow x=\pm\frac{1}{4}\)
Với \(t=\frac{5}{2}\Rightarrow\log_2\left|x\right|=\frac{5}{2}\Leftrightarrow\left|x\right|=\sqrt{32}\Leftrightarrow x=\pm\sqrt{32}\)
Vậy phương trình có 4 nghiệm : \(x=\frac{1}{4};x=-\frac{1}{4};x=\sqrt{32};x=-\sqrt{32}\)
PT
0
2 tháng 4 2017
a) Đặt t = 13x > 0 ta được phương trình:
13t2 – t – 12 = 0 ⇔ (t – 1)(13t + 12) = 0
⇔ t = 1 ⇔ 13x = 1 ⇔ x = 0
b)
Chia cả hai vế phương trình cho 9x ta được phương trình tương đương
(1+(23)x)(1+3.(23)x)=8.(23)x(1+(23)x)(1+3.(23)x)=8.(23)x
Đặt t=(23)xt=(23)x (t > 0) , ta được phương trình:
(1 + t)(1 + 3t) = 8t ⇔ 3t2 – 4t + 1 = 0 ⇔ t∈{13,1}t∈{13,1}
Với t=13t=13 ta được nghiệm x=log2313x=log2313
Với t = 1 ta được nghiệm x = 0
c) Điều kiện: x > 2
Vì nên phương trình đã cho tương đương với:
[log3(x−2)=0log5x=1⇔[x=3x=5[log3(x−2)=0log5x=1⇔[x=3x=5
d) Điều kiện: x > 0
log22x – 5log2x + 6 = 0
⇔(log2x – 2)(log2x – 3) = 0
⇔ x ∈ {4, 8}
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 1 2019
1/ ĐKXĐ: \(x>0\)
\(log_{5x}5-log_{5x}x+log_5^2x=1\)
\(\Leftrightarrow\dfrac{1}{log_55x}-\dfrac{1}{log_x5x}+log_5^2x=1\)
\(\Leftrightarrow\dfrac{1}{1+log_5x}-\dfrac{1}{1+log_x5}+log_5^2x-1=0\)
\(\Leftrightarrow\dfrac{1}{1+log_5x}-\dfrac{log_5x}{1+log_5x}+\left(log_5x-1\right)\left(log_5x+1\right)=0\)
\(\Leftrightarrow\dfrac{1-log_5x}{1+log_5x}-\left(1-log_5x\right)\left(1+log_5x\right)=0\)
\(\Leftrightarrow\left(1-log_5x\right)\left(\dfrac{1}{1+log_5x}-\left(1+log_5x\right)\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}1-log_5x=0\\\dfrac{1}{1+log_5x}=1+log_5x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}1-log_5x=0\\1+log_5x=1\\1+log_5x=-1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\\x=\dfrac{1}{25}\end{matrix}\right.\)
2/ ĐKXĐ: \(x>0\)
\(log_5\left(5^x-1\right).log_{25}\left(5^{x+1}-5\right)=1\)
\(\Leftrightarrow log_5\left(5^x-1\right).log_{5^2}5\left(5^x-1\right)=1\)
\(\Leftrightarrow log_5\left(5^x-1\right)\left(1+log_5\left(5^x-1\right)\right)=2\)
\(\Leftrightarrow log_5^2\left(5^x-1\right)+log_5\left(5^x-1\right)-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}log_5\left(5^x-1\right)=1\\log_5\left(5^x-1\right)=-2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}5^x-1=5\\5^x-1=\dfrac{1}{25}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}5^x=6\\5^x=\dfrac{26}{25}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=log_56\\x=log_5\dfrac{26}{25}\end{matrix}\right.\)
3/ ĐKXĐ: \(x>0\)
\(2log_3^2x-log_3x.log_3\left(\sqrt{2x+1}-1\right)=0\)
\(\Leftrightarrow log_3x\left(2log_3x-log_3\left(\sqrt{2x+1}-1\right)\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}log_3x=0\Rightarrow x=1\\2log_3x-log_3\left(\sqrt{2x+1}-1\right)=0\left(1\right)\end{matrix}\right.\)
Xét (1): \(log_3x^2=log_3\left(\sqrt{2x+1}-1\right)\Leftrightarrow x^2=\sqrt{2x+1}-1\)
\(\Leftrightarrow x^2+1=\sqrt{2x+1}\Leftrightarrow x^4+2x^2+1=2x+1\)
\(\Leftrightarrow x^4+2x^2-2x=0\Leftrightarrow x\left(x^3+2x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(l\right)\\x^3+2x-2=0\end{matrix}\right.\) ????
Pt bậc 3 kia có nghiệm rất xấu, chỉ giải được bằng công thức Cardano mà bậc phổ thông không học, nên bạn có chép đề sai không vậy?
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2023
\(=\left(log_{a^{-1}}a^2\right)^2+\dfrac{1}{2}.\dfrac{1}{2}log_aa\)
\(=\left(-1.2.log_aa\right)^2+\dfrac{1}{4}=4+\dfrac{1}{4}=\dfrac{17}{4}\)
