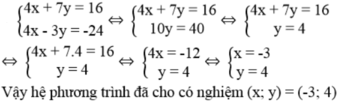K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CH
Cô Hoàng Huyền
Admin
VIP
3 tháng 4 2017
Ta tách như sau:
\(a^2+b^2+3ab-8a-8b-2\sqrt{3ab}+19=0\)
\(\Leftrightarrow a^2+b^2+2ab-8a-8b+ab-2\sqrt{3ab}+3+16=0\)
\(\Leftrightarrow\left(a+b\right)^2-8\left(a+b\right)+\left(\sqrt{ab}-\sqrt{3}\right)^2+16=0\)
\(\Leftrightarrow\left[\left(a+b\right)^2-2.\left(a+b\right).4+16\right]+\left(\sqrt{ab}-\sqrt{3}\right)^2=0\)
\(\Leftrightarrow\left(a+b-4\right)^2+\left(\sqrt{ab}-\sqrt{3}\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}a+b-4=0\\\sqrt{ab}=\sqrt{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}a+b=4\\ab=3\end{cases}}\)
Vậy thì phương trình bậc hai có nghiệm a và b là: \(x^2-4x+3=0\).
NN
1
NA
0
17 tháng 8 2019
ĐK x bất kì
\(\sqrt{x^2+24}=24-x^4\)
\(\Leftrightarrow x^2+24=576-48x^4+x^8\)
\(\Leftrightarrow x^8-48x^4-x^2+552=0\)
Giải ra là tìm được x
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
Bạn xem lại đề, nghiệm của hệ này rất xấu (chính xác là ko thể giải được nếu ko áp dụng công thức nghiệm Cardano của pt bậc 3)