K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
13 tháng 10 2021
Bạn chỉ cần áp dụng cái phân tích đa thức thành nhân tử bằng phương pháo đặt nhân tử chung là ra rồi
MA
2
15 tháng 11 2021
\(d,=\dfrac{3y}{5x\left(x-y\right)}\\ e,=\dfrac{5x\left(x+2\right)\left(2-x\right)}{4\left(x-2\right)\left(x+2\right)}=\dfrac{-5x}{4}\\ f,=\dfrac{3\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)\left(6-x\right)}=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\\ g,=\dfrac{3xy\left(x-3y\right)\left(x+3y\right)}{2x^2y^2\left(x-3y\right)}=\dfrac{3\left(x+3y\right)}{2xy}\\ h,=\dfrac{45x^2y\left(x-y\right)\left(x+y\right)}{10xy\left(y-x\right)}=\dfrac{-9x\left(x+y\right)}{2}\\ i,=\dfrac{12\left(a-b\right)\left(a+b\right)\left(a^2+ab+b^2\right)}{3\left(a+b\right)\left(a-b\right)^2}=\dfrac{4\left(a^2+ab+b^2\right)}{a-b}\)
15 tháng 11 2021
e: \(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-10}{4}=-\dfrac{5}{2}\)
23 tháng 9 2021
40: Ta có: \(A=27x^3+8y^3-3x-2y\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)-\left(3x+2y\right)\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2-1\right)\)
11 tháng 7 2021
24: Ta có: \(A=10ax-5ay+2x-y\)
\(=5a\left(2x-y\right)+\left(2x-y\right)\)
\(=\left(2x-y\right)\left(5a+1\right)\)
25: Ta có: \(A=10ax-5ay-2x+y\)
\(=5a\left(2x-y\right)-\left(2x-y\right)\)
\(=\left(2x-y\right)\left(5a-1\right)\)
30 tháng 4 2022
e: \(\dfrac{12-3x}{2x+6}-3>0\)
\(\Leftrightarrow\dfrac{12-3x-6x-18}{2x+6}>0\)
\(\Leftrightarrow\dfrac{-9x+6}{2x+6}>0\)
\(\Leftrightarrow\dfrac{3x-2}{x+3}< 0\)
=>-3<x<2/3
12 tháng 3 2022
Câu 3e
\(\left(2x+1\right)^2=\left(x-1\right)^2\)
\(\left[{}\begin{matrix}2x+1=x-1\\2x+1=1-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=0\end{matrix}\right.\)
4 tháng 8 2023
c: Xét ΔANB có
EM//NB
E là trung điểm của AB
=>M là trung điểm của AN
=>AM=MN
Xét ΔDMC có
F là trung điểm của CD
FN//DM
=>N là trung điểm của CM
=>CN=NM=AM
AM+MO=AO
CN+NO=CO
mà AO=CO và AM=Cn
nên MO=NO
=>O là trung điểm của MN
=>M đối xứng N qua O
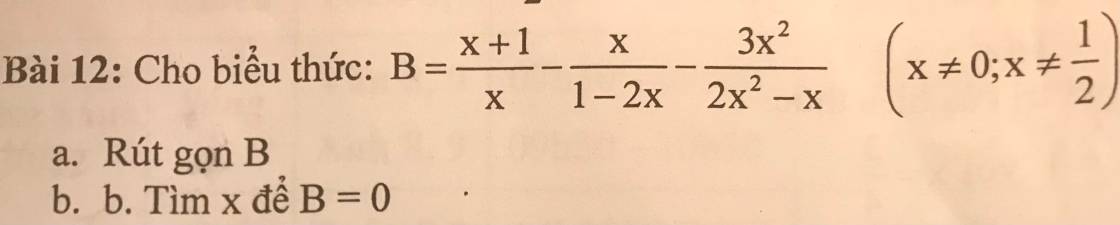
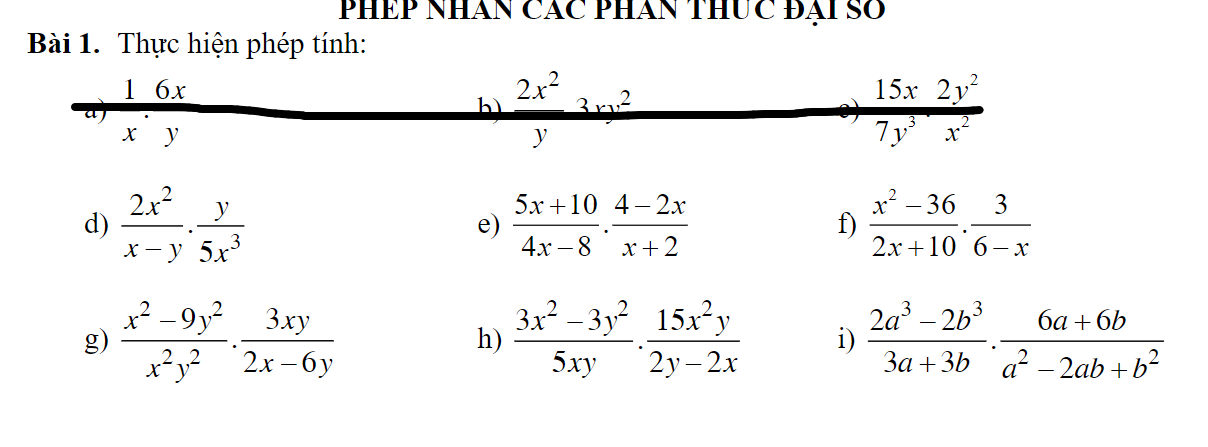
a: \(=\dfrac{\left(x+1\right)\left(2x-1\right)+x^2-3x^2}{x\left(2x-1\right)}\)
\(=\dfrac{2x^2-x+2x-1+\left(-2x^2\right)}{x\left(2x-1\right)}\)
\(=\dfrac{x-1}{x\left(2x-1\right)}\)
b: Để B=0 thì x-1=0
=>x=1