K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 10 2021
\(C=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{4\sqrt{x}}{x-1}\)
\(\Rightarrow C=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow C=\dfrac{x+2\sqrt{x}+1-4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow C=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow C=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow C=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
2
22 tháng 5 2022
`a)A` có nghĩa `<=>x-1 >= 0 <=>x >= 1`
`b)B=\sqrt{3^2 .2}+\sqrt{2^3}-\sqrt{5^2 .2}`
`<=>B=3\sqrt{2}+2\sqrt{2}-5\sqrt{2}`
`<=>B=0`
`c)` Với `a >= 0,a \ne 1` có:
`C=[a-1]/[\sqrt{a}-1]-[a\sqrt{a}-1]/[a-1]`
`C=[(a-1)(\sqrt{a}+1)-a\sqrt{a}+1]/[(\sqrt{a}-1)(\sqrt{a}+1)]`
`C=[a\sqrt{a}+a-\sqrt{a}-1-a\sqrt{a}+1]/[(\sqrt{a}-1)(\sqrt{a}+1)]`
`C=a/[a-1]`
S
23 tháng 10 2021
Bài 2:
\(a.\left(5-a\right)\sqrt{\dfrac{8a}{a-5}}\\ a>5 \\= \sqrt{\dfrac{8a\left(5-a\right)^2}{a-5}}\\ =\sqrt{\dfrac{8a\left(a-5\right)^2}{a-5}}\\ =\sqrt{8a\left(a-5\right)}=\sqrt{8a^2-40}\\b.\left(x-7\right)\sqrt{\dfrac{\left(x+7\right)}{49-x^2}}\\ =\left(x-7\right)\sqrt{\dfrac{\left(x+7\right)}{\left(7-x\right)\left(x+7\right)}}\\ \left(x-7\right)\sqrt{\dfrac{1}{7-x}}\\ =\sqrt{\dfrac{\left(x-7\right)^2}{7-x}}=\sqrt{\dfrac{\left(7-x\right)^2}{7-x}}\\ =\sqrt{7-x}\\ c.\)
\(\dfrac{a}{b}\sqrt{\dfrac{b}{a}}\\ a,b>0 \\ =\sqrt{\dfrac{a^2b}{b^2a}}=\sqrt{\dfrac{a}{b}}\\ d.x\sqrt{\dfrac{6}{x}}\\ x>0\\ =\sqrt{\dfrac{6x^2}{x}}=\sqrt{6x}\)
S
23 tháng 10 2021
Bài 3:
\(a.7\sqrt{2}=\sqrt{7^2.2}=\sqrt{98}\)
Vì \(\sqrt{98}>\sqrt{72}\Rightarrow7\sqrt{2}>\sqrt{72}\)
\(b.4\sqrt[]{3}=\sqrt{4^2.3}=\sqrt{48}\\ 3\sqrt{5}=\sqrt{3^2.5}=\sqrt{45}\)
vì: \(48>45\Rightarrow\sqrt{48}>\sqrt{45}\Rightarrow4\sqrt{3}>3\sqrt{5}\)
c.\(4\sqrt{7}=\sqrt{4^2.7}=\sqrt{112}\\ 5\sqrt{6}=\sqrt{5^2.6}=\sqrt{150}\)
Vì: \(112< 150\Rightarrow\sqrt{112}< \sqrt{150}\Rightarrow4\sqrt{7}< 5\sqrt{6}\)
d.\(\dfrac{1}{6}\sqrt{18}=\sqrt{\dfrac{18}{6^2}}=\sqrt{\dfrac{18}{36}}=\sqrt{\dfrac{1}{2}}\\ \dfrac{1}{2}\sqrt{2}=\sqrt{\dfrac{2}{4}}=\sqrt{\dfrac{1}{2}}\)
Vì: \(\dfrac{1}{2}=\dfrac{1}{2}\Rightarrow\sqrt{\dfrac{1}{2}}=\sqrt{\dfrac{1}{2}}\Rightarrow\dfrac{1}{6}\sqrt{15}=\dfrac{1}{2}\sqrt{2}\)
ML
0
18 tháng 9 2021
a) \(x^2-15=\left(x-\sqrt{15}\right)\left(x+\sqrt{15}\right)\)
d) \(x-6\sqrt{x}+9-\left(\sqrt{x}-1\right)^2=\left(\sqrt{x}-3\right)^2-\left(\sqrt{x}-1\right)^2=\left(\sqrt{x}-3-\sqrt{x}+1\right)\left(\sqrt{x}-3+\sqrt{x}-1\right)=-2\left(2\sqrt{x}-4\right)=-4\left(\sqrt{x}-2\right)\)
DG
5 tháng 11 2017
AB trước nha
Phương trình đường thẳng cần tìm có dạng y =ax + b
Qua A (2;4) => (thế x và y vào hpt nha ) 4= 2a + b (1)
Qua B(3;6) => 6= 3a+ b (2)
Rút b ra <=> b = 6-3a
Thế b vào (1)
<=> 4= 2a + 6-3a
a =2 ( chắc đúng)
Thế vào (2)
<=> 6= 3×2 + b
b = 0
Vậy hàm số AB cần tìM y= ax + b
<=> Y= 2x + 0(2x thui CX đc)
Vẽ BC
Qua điểm C(7;2) <=>2= 7a+ b
Thế b tìm đc ở điểm B
<=> 2 = 7a + 0
a = 2/7
Vậy hàm số BC cần tìm y= 2/7x
Làm tương tự như (1) và (2)
Thế vào thì hàm số AC cần tìm là
Y= -2/5x
Chắc đúng
30 tháng 6 2023
1:
d: P=A+B
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{x-25}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+3}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}+3}=\dfrac{2\sqrt{x}+1}{\sqrt{x}+3}\)
P nguyên
=>2căn x+6-5 chia hết cho căn x+3
=>căn x+3 thuộc Ư(-5)
=>căn x+3=5
=>x=4
3:
2:
b: PTHĐGĐ là:
x^2-2(m+1)x+2m+1=0
Theo đề, ta có:
x1^2+x2^2=(căn 5)^2=5
=>(x1+x2)^2-2x1x2=5
=>(2m+2)^2-2(2m+1)=5
=>4m^2+8m+4-4m-2-5=0
=>4m^2+4m+1=0
=>m=-1/2
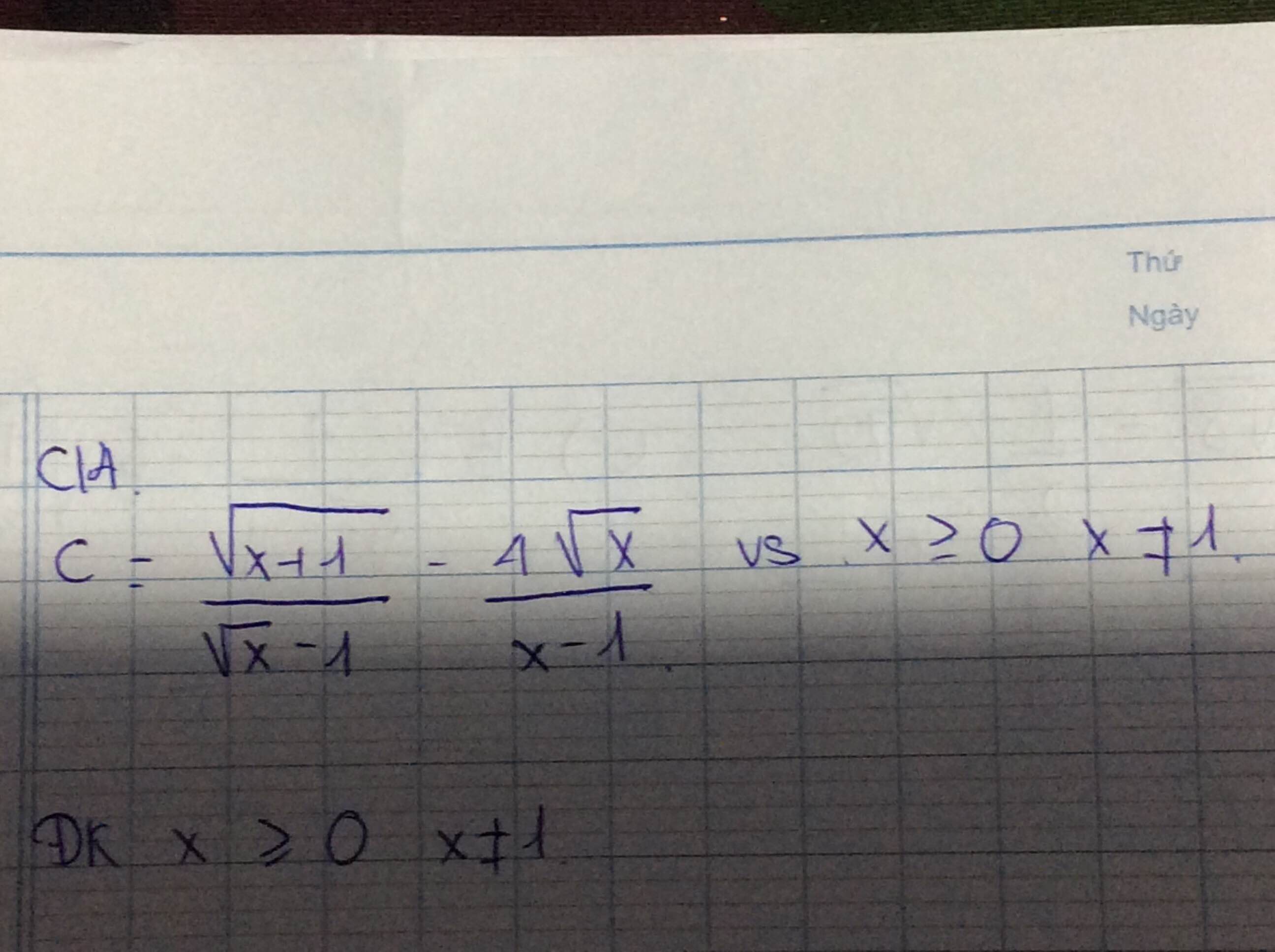
Lời giải:
c. Đặt $\sqrt{x}=a; \sqrt{y}=b$ thì:
$C=a^3-b^3+a^2b-ab^2=(a-b)(a^2+ab+b^2)+ab(a-b)$
$=(a-b)(a^2+ab+b^2+ab)=(a-b)(a^2+2ab+b^2)$
$=(a-b)(a+b)^2=(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})^2$