K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 11 2021
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
a.
Khi \(x=4\Rightarrow A=\dfrac{1}{\sqrt{4}}+\dfrac{\sqrt{4}}{\sqrt{4}+1}=\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{7}{6}\)
b.
\(B=\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}}=\dfrac{1}{3}\)
\(\Rightarrow3\sqrt{x}=x+\sqrt{x}\)
\(\Rightarrow x-2\sqrt{x}=0\)
\(\Rightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
c.
\(P=A:B=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{x+\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P>3\Rightarrow\dfrac{x+\sqrt{x}+1}{\sqrt{x}}>3\)
\(\Leftrightarrow x+\sqrt{x}+1>3\sqrt{x}\) (do \(\sqrt{x}>0\))
\(\Leftrightarrow x-2\sqrt{x}+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2>0\)
\(\Leftrightarrow\sqrt{x}-1\ne0\)
\(\Rightarrow x\ne1\)
Kết hợp ĐKXĐ ta được: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
21 tháng 12 2022
anh ơi https://hoc24.vn/cau-hoi/giai-phuong-trinh-nghiem-nguyen-saux2x-y20.1353640161947
-> giải thích hộ cái bảng của a tính thế nào vs ạ
TH
1
16 tháng 6 2023
2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40
8 tháng 12 2021
2: Tọa độ là:
\(\left\{{}\begin{matrix}2x+1=x-3\\y=x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-7\end{matrix}\right.\)
8 tháng 11 2023
4:
a: vì a=2>0
nên hàm số y=2x-1 đồng biến trên R
b:
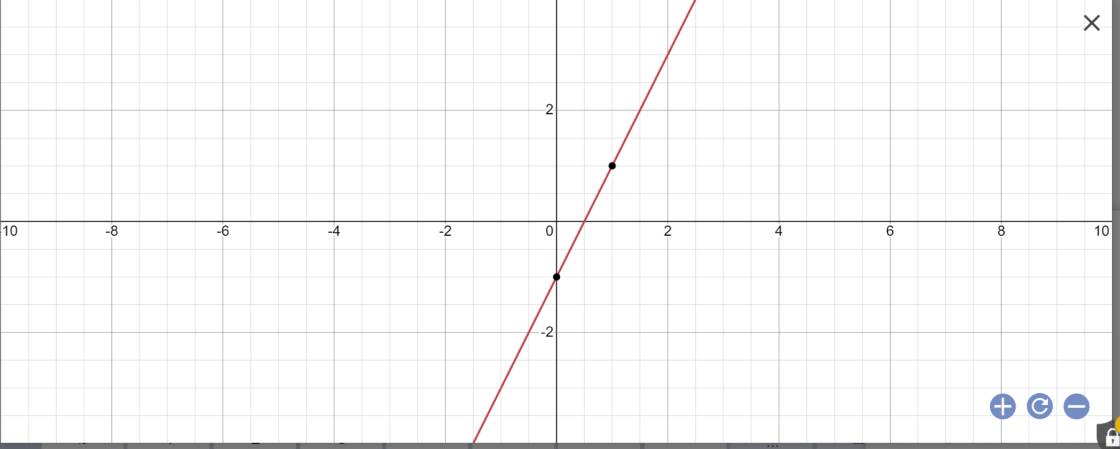
c: Thay x=1 vào y=2x-1, ta được:
\(y=2\cdot1-1=2-1=1\)
=>A(1;1) có thuộc (d)
d: Phương trình hoành độ giao điểm là:
2x-1=-x+2
=>\(2x+x=2+1\)
=>3x=3
=>x=1
Thay x=1 vào y=2x-1, ta được:
\(y=2\cdot1-1=1\)
Vậy: (d) cắt (d') tại A(1;1)
e: Vì (m): y=ax+b song song với (d) nên ta có:
\(\left\{{}\begin{matrix}a=2\\b< >-1\end{matrix}\right.\)
=>y=2x+b
Thay x=-2 và y=3 vào y=2x+b, ta được:
b-2*2=3
=>b-4=3
=>b=7
=>y=2x+7
10 tháng 12 2023
16c:
ĐKXĐ: \(x>=3\)
\(\sqrt{x^2-9}+6=3\sqrt{x+3}+\sqrt{x-3}\)
Đặt \(\sqrt{x-3}=a\left(a>=0\right);\sqrt{x+3}=b\left(b>=0\right)\)
Phương trình sẽ trở thành:
ab+6=3b+a
=>\(ab-a-3b-6=0\)
=>\(\left(ab-3b\right)-a+3-9=0\)
=>\(b\left(a-3\right)-\left(a-3\right)=9\)
=>\(\left(a-3\right)\left(b-1\right)=9\)
=>\(\left(a-3\right)\left(b-1\right)=1\cdot9=9\cdot1=\left(-1\right)\cdot\left(-9\right)=\left(-9\right)\cdot\left(-1\right)=3\cdot3=\left(-3\right)\cdot\left(-3\right)\)(1)
a>=0; b>=0
=>a-3>=-3; b-1>=-1(2)
Từ (1) và (2) suy ra
\(\left(a-3;b-1\right)\in\left\{\left(1;9\right);\left(9;1\right);\left(3;3\right)\right\}\)
=>\(\left(a,b\right)\in\left\{\left(4;10\right);\left(12;2\right);\left(6;4\right)\right\}\)
TH1: a=4 và b=10
=>\(\left\{{}\begin{matrix}\sqrt{x-3}=4\\\sqrt{x+3}=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-3=16\\x+3=100\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=19\\x=97\end{matrix}\right.\)
=>Loại
TH2: a=12 và b=2
=>\(\left\{{}\begin{matrix}\sqrt{x-3}=12\\\sqrt{x+3}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-3=144\\x+3=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=147\\x=1\end{matrix}\right.\)
=>Loại
TH3: a=6 và b=4
=>\(\left\{{}\begin{matrix}\sqrt{x-3}=6\\\sqrt{x+3}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-3=36\\x+3=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=39\\x=13\end{matrix}\right.\)
=>Loại
vậy: Phương trình vô nghiệm
10 tháng 12 2023
Phóng to cho tôi xem , bài của cậu chữ bé nhỏ tôi ko nhìn thấy gì cả?
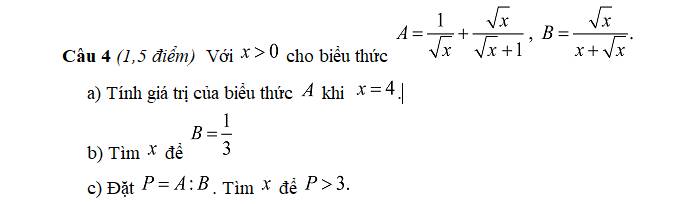
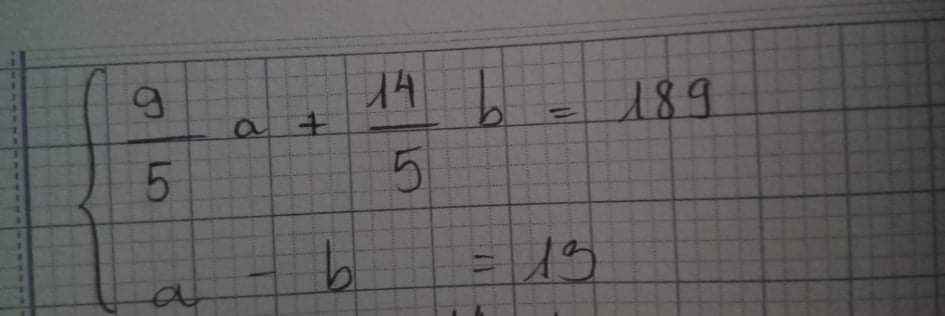
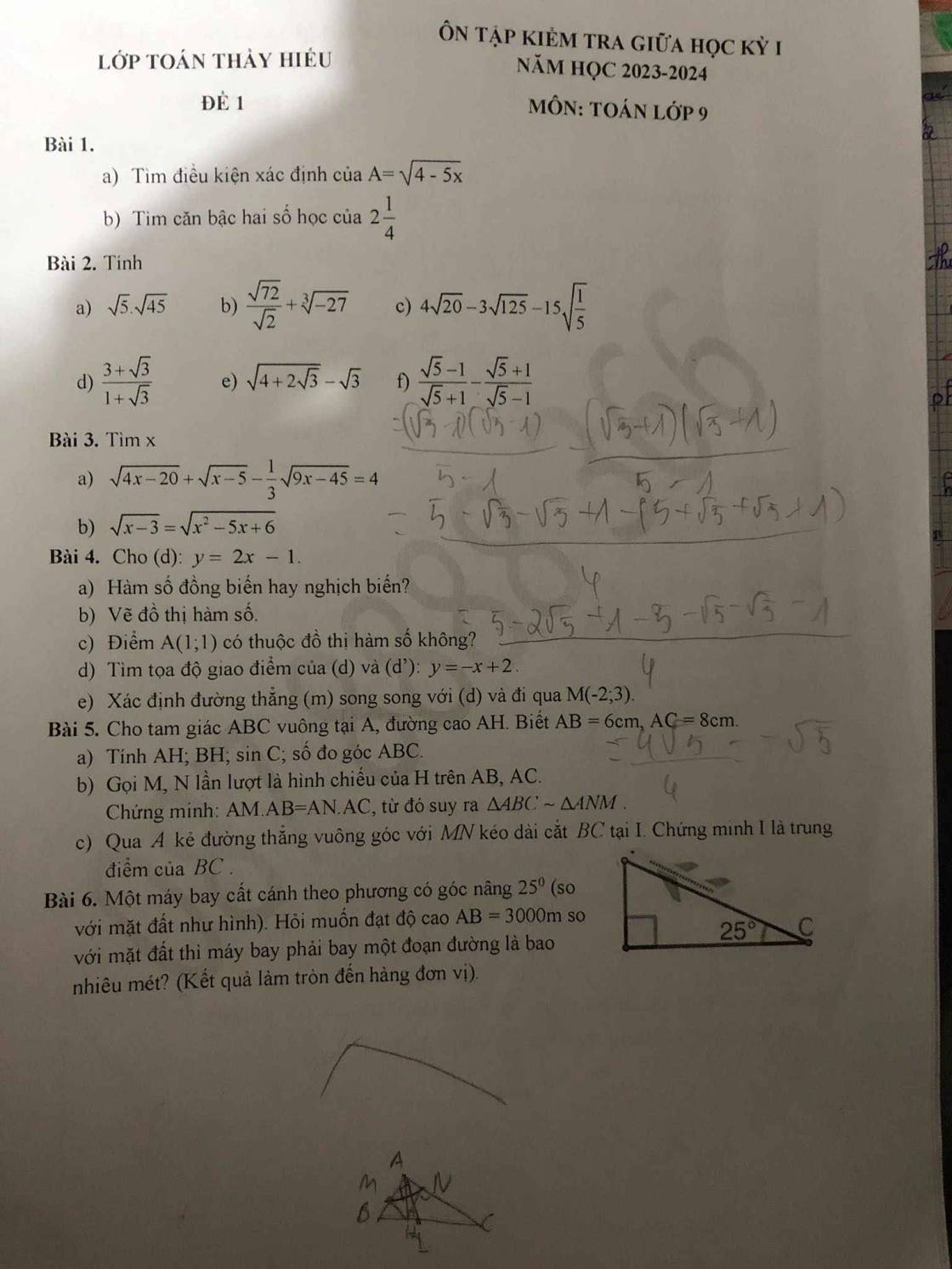
Gọi số học sinh nam là x
Số học sinh nữ là 32-x
Vì khi chuyển 4 nữ đi thì số nam và số nữ bằng nhau nên ta có:
32-x-4=x
=>28-x=x
=>x=14
Vậy: Có 14 nam và 18 nữ