K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 12 2022
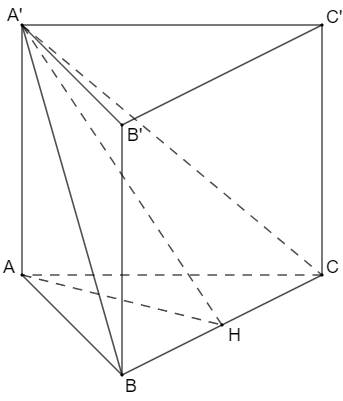
Góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 600
\(\Rightarrow\widehat{A'HA}=60^\circ\)
Tam giác AA'H vuông tại A: \(AH=AA'.cot60^\circ=\dfrac{2a\sqrt{3}}{3}\)
Tam giác ABC đều nên \(AH=\dfrac{BC\sqrt{3}}{2}\) \(\Rightarrow BC=\dfrac{4a}{3}\)
Thể tích khối lăng trụ là: \(V=\dfrac{1}{2}AH\cdot BC\cdot AA'=\dfrac{8\sqrt{3}}{9}a^3\).
19 tháng 12 2022
\(g'\left(x\right)=f'\left(x\right)f\left(f\left(x\right)\right)=0\Leftrightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f\left(f\left(x\right)\right)=0\end{matrix}\right.\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(f\left(f\left(x\right)\right)=0\Leftrightarrow\left[{}\begin{matrix}f\left(x\right)=x_1\left(x_1< -1\right)\\f\left(x\right)=1\end{matrix}\right.\)
\(f\left(x\right)=x_1\left(x_1< -1\right):\) phương trình có 1 nghiệm.
\(f\left(x\right)=1:\) phương trình có 3 nghiệm.
Số nghiệm của phương trình \(g'\left(x\right)=0\) là 6.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
ĐKXĐ: \(x>1\)
\(2log_5\left(x-1\right)-log_5\left(4x+m\right)=0\)
\(\Rightarrow log_5\left(x-1\right)^2=log_5\left(4x+m\right)\)
\(\Rightarrow\left(x-1\right)^2=4x+m\)
\(\Rightarrow m=x^2-6x+1\)
Xét hàm \(f\left(x\right)=x^2-6x+1\) với \(x>1\)
\(f'\left(x\right)=2x-6=0\Rightarrow x=3\)
\(f\left(1\right)=-4\) ; \(f\left(3\right)=-8\)
\(\Rightarrow\) Pt có 2 nghiệm pb thỏa mãn \(x>1\) khi \(-8< m< -4\)
\(\Rightarrow m=\left\{-7;-6;-5\right\}\) có 3 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
\(f'\left(x\right)=x^2\left(x+2\right)\) có đúng 1 nghiệm bội lẻ \(x=-2\)
\(y=f\left(x^3-3x\right)\Rightarrow y'=\left(3x^2-3\right).f'\left(x^3-3x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3x^2-3=0\\x^3-3x=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2-1=0\\\left(x-1\right)^2\left(x+2\right)=0\end{matrix}\right.\)
\(\Rightarrow x=\left\{-1;1;-2\right\}\) hàm có 3 điểm cực trị
20 tháng 12 2022
Đặt \(3^x=t,\left(t>0\right)\)
Phương trình đã cho trở thành: \(t^2-2\left(m-1\right)t+2m+1=0\) (2)
Yêu cầu bài toán tương đương với phương trình (2) có hai nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(m-1\right)^2-2m-1>0\\t_1+t_2=2\left(m-1\right)>0\\t_1\cdot t_2=2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>4\end{matrix}\right.\\m>1\\m< -\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m>4\)
20 tháng 12 2022
Hàm số có tập xác định là \(ℝ\) \(\Leftrightarrow x^2-2x-m+1>0\forall x\inℝ\)
\(\Leftrightarrow\Delta'=1-\left(-m+1\right)< 0\)
\(\Leftrightarrow m< 0\)
\(m\in\left(-2021;2021\right)\), m nguyên nên có 2020 giá trị của m thỏa mãn.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
\(y'=x^2+2mx+2m\)
Hàm đồng biến trên R khi và chỉ khi \(y'\ge0;\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=m^2-2m\le0\end{matrix}\right.\)
\(\Rightarrow0\le m\le2\)
Có 2 giá trị nguyên dương của m thỏa mãn (1 và 2)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
Giả sử (P) cắt đáy nón theo đoạn thẳng AB
Độ dài AB là: \(2\left(1+\sqrt{5}\right)a-2.a\sqrt{5}=2a\)
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\)
\(AH=\dfrac{1}{2}AB=a\); \(SO=\sqrt{\left(a\sqrt{5}\right)^2-\left(2a\right)^2}=a\)
\(OH=\sqrt{R^2-AH^2}=a\sqrt{3}\)
Từ O kẻ \(OK\perp SH\Rightarrow OK=d\left(O;\left(P\right)\right)\)
Áp dụng hệ thức lượng trong tam giac vuông SOH:
\(\dfrac{1}{OK^2}=\dfrac{1}{SO^2}+\dfrac{1}{OH^2}=\dfrac{4}{3a^2}\Rightarrow OK=\dfrac{a\sqrt{3}}{2}\)
20 tháng 12 2022
TCĐ: \(x=-1\Rightarrow b=-1\).
TCN: \(y=2\Rightarrow a=2\).
\(a+b=1\).
Chọn A.
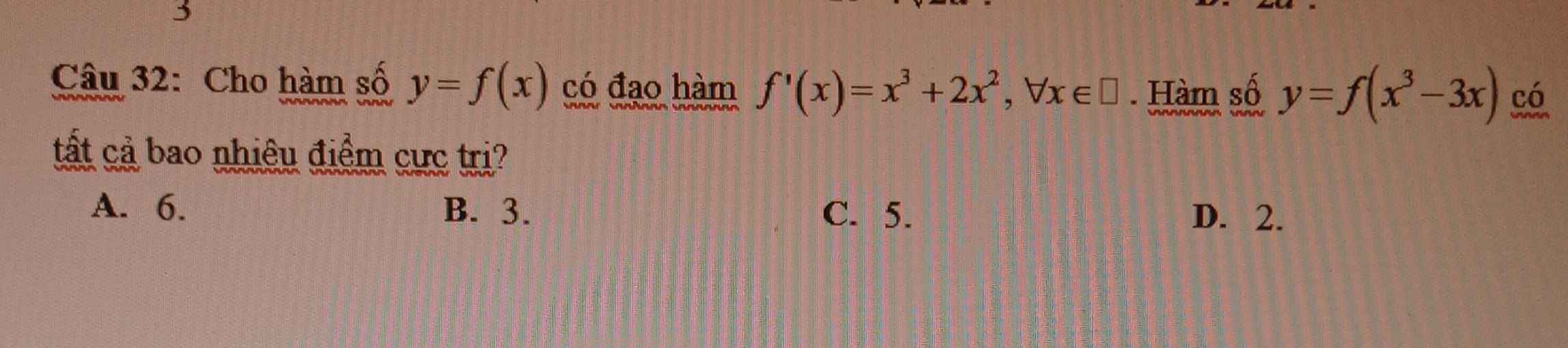
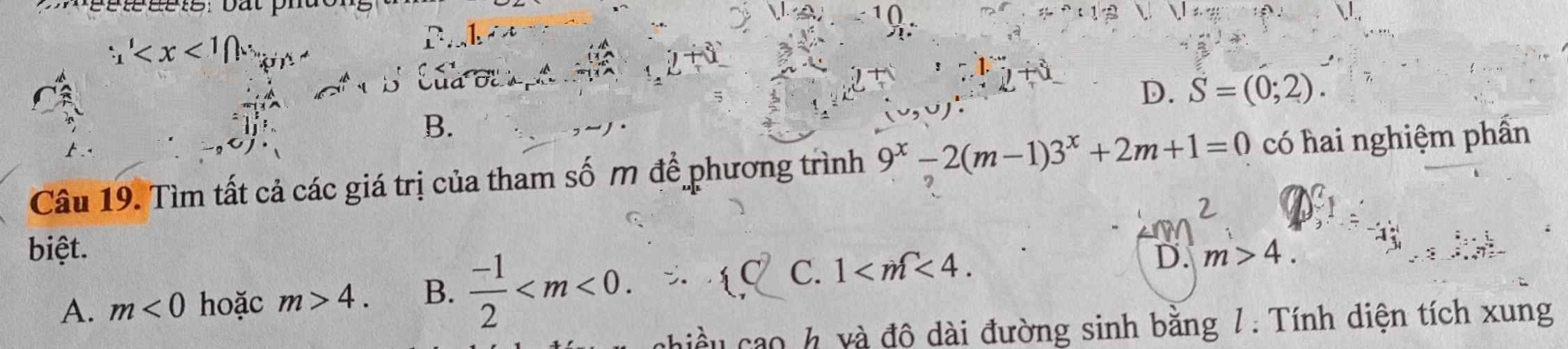
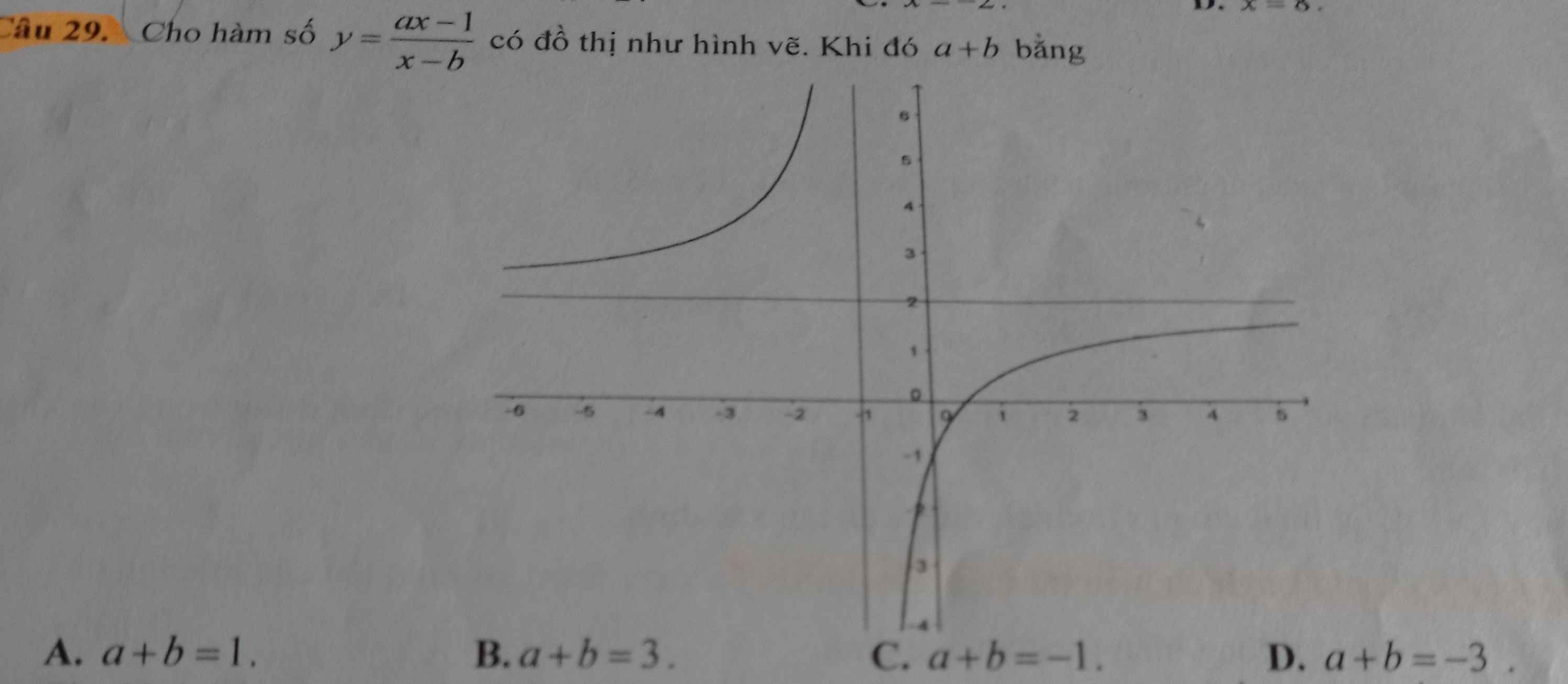
\(V_{OABC}=\dfrac{1}{6}OA.OB.OC=\dfrac{2a^3}{3}\)
\(AC=\sqrt{OA^2+AC^2}=a\sqrt{5}\)
Trong tam giác vuông OAC: \(OA^2=AH.AC\Rightarrow AH=\dfrac{OA^2}{AC}=\dfrac{OA^2}{\sqrt{OA^2+OC^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{1}{5}\)
Do I là trung điểm AB \(\Rightarrow\dfrac{AI}{AB}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{V_{AOIH}}{V_{OABC}}=\dfrac{\dfrac{1}{3}d\left(O;\left(ABC\right)\right).\dfrac{1}{2}AH.AI.sin\widehat{BAC}}{\dfrac{1}{3}d\left(O;\left(ABC\right)\right).\dfrac{1}{2}AC.AB.sin\widehat{BAC}}=\dfrac{AH}{AC}.\dfrac{AI}{AB}=\dfrac{1}{10}\)
\(\Rightarrow V_{AOIH}=\dfrac{1}{10}.\dfrac{2a^3}{3}=\dfrac{a^3}{15}\)