K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2022
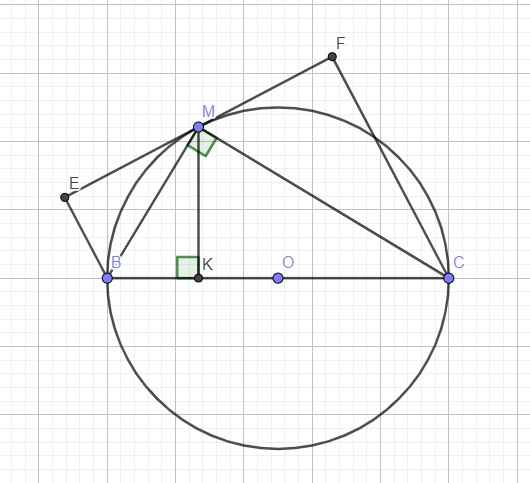
\(\widehat{BME}=\widehat{BMK}\) (do K đối xứng E qua MB)
Mà \(\widehat{BMK}=\widehat{BCM}\) (cùng phụ \(\widehat{MBC}\))
\(\Rightarrow\widehat{BME}=\widehat{BCM}\)
\(\Rightarrow ME\) là tiếp tuyến của (O) tại M
Tương tự, ta có MF là tiếp tuyến của (O) tại M
\(\Rightarrow M;E;F\) thẳng hàng
\(\Rightarrow S_{BEFC}=S_{BEMK}+S_{CFMK}=2S_{BMK}+2S_{CMK}=2S_{MBC}\)
Mà \(S_{MBC}=\dfrac{1}{2}MK.BC\Rightarrow S_{MBC-max}\) khi \(MK_{max}\)
\(\Rightarrow M\) nằm chính giữa cung BC \(\Rightarrow MK_{max}=R=4\left(cm\right)\)
\(\Rightarrow S_{BEFC-max}=2.\dfrac{1}{2}.4.8=32\left(cm^2\right)\)
10 tháng 4 2022
để A là số nguyên thì \(x-9-5⋮\sqrt{x}+3\)
\(\Leftrightarrow\sqrt{x}+3\inƯ\left(5\right)\)
\(\Leftrightarrow\sqrt{x}+3=5\)
hay x=4
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2022
TH1: \(x=14\Rightarrow A=0\) (thỏa mãn)
TH2: \(x\ne14\Rightarrow A\) nguyên khi \(x\) là SCP và \(\dfrac{x-14}{\sqrt{x}+3}\in Z\Rightarrow\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)-5}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}-3-\dfrac{5}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\dfrac{5}{\sqrt{x}+3}\in Z\Rightarrow\sqrt{x}+3=Ư\left(5\right)=5\) (do \(\sqrt{x}+3\ge3\))
\(\Rightarrow x=4\)
Vậy \(x=\left\{4;14\right\}\) có 2 giá trị
TH
1
16 tháng 6 2023
2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2022
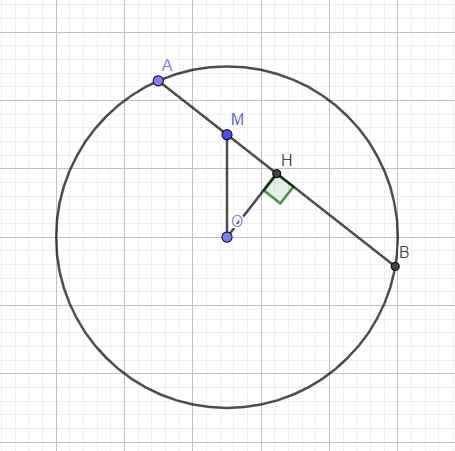
Gọi AB là dây cung qua M, H là trung điểm AB \(\Rightarrow OH\perp AB\) và \(OH\le OM=3\)
Áp dụng định lý Pitago:
\(OH^2+AH^2=OA^2=25\)
\(\Rightarrow AB=2AH=2\sqrt{25-OH^2}\)
AB nguyên khi \(25-OH^2=\dfrac{k^2}{4}\)
\(\Rightarrow OH^2=25-\dfrac{k^2}{4}\)
\(0\le OH\le3\Rightarrow0\le OH^2\le9\)
\(\Rightarrow0\le25-\dfrac{k^2}{4}\le9\)
\(\Rightarrow64\le k^2\le100\Rightarrow8\le k\le10\)
\(\Rightarrow k=\left\{8;9;10\right\}\) có 3 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2022
Gọi chiều dài của mảnh đất là x (25<x<50)
Chiều rộng của mảnh đất là: \(50-x\) (m)
Diện tích mảnh đất ban đầu: \(x\left(50-x\right)\)
Chiều dài và chiều rộng mảnh đất sau khi mở lối đi lần lượt là: \(x-2\) và \(48-x\)
Diện tích phần đất trồng rau: \(\left(x-2\right)\left(48-x\right)\)
Ta có pt:
\(\left(x-2\right)\left(48-x\right)=\dfrac{84}{100}x\left(50-x\right)\)
\(\Rightarrow x^2-50x+600=0\Rightarrow\left[{}\begin{matrix}x=20\left(loại\right)\\x=30\end{matrix}\right.\)
Vậy chiều rộng mảnh đất là 20 (m)
MH
9 tháng 4 2022
Gọi phương trình đường thẳng đi qua 2 điểm \(A,B\) là \(y=mx+n\)
Do \(\left\{{}\begin{matrix}A\in AB\\B\in AB\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow AB:y=-2x+1\)
Do \(C\left(a,b\right)\in\left(d\right):y=2x-3\Rightarrow b=2a-3\) (1)
Mặt khác, để \(A,B,C\) thẳng hàng thì \(C\in AB\Rightarrow b=-2a+1\) (2)
Từ (1) và (2) ta có \(a=1,b=-1\) nên \(a+b=0\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2022
Do C thuộc d nên: \(b=2a-3\) \(\Rightarrow C\left(a;2a-3\right)\)
Gọi phương trình đường thẳng d1 qua 2 điểm A; B có dạng:
\(y=mx+n\)
A; B thuộc d1 nên: \(\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow\) Phương trình d1: \(y=-2x+1\)
A;B;C thẳng hàng khi và chỉ khi C thuộc d1
\(\Rightarrow2a-3=-2a+1\)
\(\Rightarrow4a=4\Rightarrow a=1\Rightarrow b=-1\)
\(\Rightarrow a+b=0\)
5 tháng 8 2021
22,
1, Đặt √(3-√5) = A
=> √2A=√(6-2√5)
=> √2A=√(5-2√5+1)
=> √2A=|√5 -1|
=> A=\(\dfrac{\sqrt{5}-1}{\text{√2}}\)
=> A= \(\dfrac{\sqrt{10}-\sqrt{2}}{2}\)
2, Đặt √(7+3√5) = B
=> √2B=√(14+6√5)
=> √2B=√(9+2√45+5)
=> √2B=|3+√5|
=> B= \(\dfrac{3+\sqrt{5}}{\sqrt{2}}\)
=> B= \(\dfrac{3\sqrt{2}+\sqrt{10}}{2}\)
3,
Đặt √(9+√17) - √(9-√17) -\(\sqrt{2}\)=C
=> √2C=√(18+2√17) - √(18-2√17) -\(2\)
=> √2C=√(17+2√17+1) - √(17-2√17+1) -\(2\)
=> √2C=√17+1- √17+1 -\(2\)
=> √2C=0
=> C=0
26,
|3-2x|=2\(\sqrt{5}\)
TH1: 3-2x ≥ 0 ⇔ x≤\(\dfrac{-3}{2}\)
3-2x=2\(\sqrt{5}\)
-2x=2\(\sqrt{5}\) -3
x=\(\dfrac{3-2\sqrt{5}}{2}\) (KTMĐK)
TH2: 3-2x < 0 ⇔ x>\(\dfrac{-3}{2}\)
3-2x=-2\(\sqrt{5}\)
-2x=-2√5 -3
x=\(\dfrac{3+2\sqrt{5}}{2}\) (TMĐK)
Vậy x=\(\dfrac{3+2\sqrt{5}}{2}\)
6 tháng 8 2021
2, \(\sqrt{x^2}\)=12 ⇔ |x|=12 ⇔ x=12, -12
3, \(\sqrt{x^2-2x+1}\)=7
⇔ |x-1|=7
TH1: x-1≥0 ⇔ x≥1
x-1=7 ⇔ x=8 (TMĐK)
TH2: x-1<0 ⇔ x<1
x-1=-7 ⇔ x=-6 (TMĐK)
Vậy x=8, -6
4, \(\sqrt{\left(x-1\right)^2}\)=x+3
⇔ |x-1|=x+3
TH1: x-1≥0 ⇔ x≥1
x-1=x+3 ⇔ 0x=4 (KTM)
TH2: x-1<0 ⇔ x<1
x-1=-x-3 ⇔ 2x=-2 ⇔x=-1 (TMĐK)
Vậy x=-1
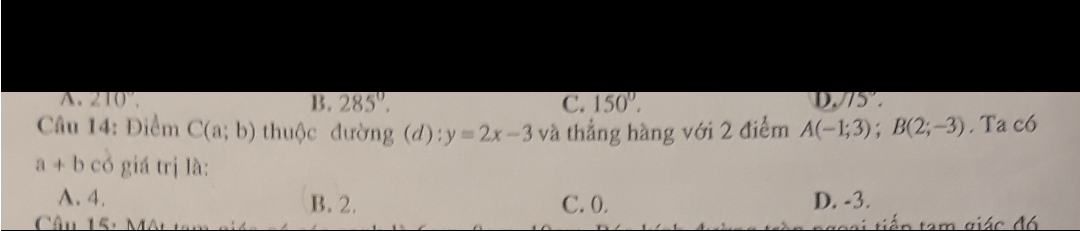
Chọn C