Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(x^4-x^2+\dfrac{1}{4}-\dfrac{225}{4}=0\\ \left(x^2-\dfrac{1}{2}\right)^2-\dfrac{15}{2}^2=0\\ \left(x+7\right)\left(x-8\right)=0\\ \left[{}\begin{matrix}x=8\\x=-7\end{matrix}\right.\)
Vậy x = 8 hoặc x = -7
a: Ta có: \(x^4-x^2-56=0\)
\(\Leftrightarrow x^4-8x^2+7x^2-56=0\)
\(\Leftrightarrow\left(x^2-8\right)\left(x^2+7\right)=0\)
\(\Leftrightarrow x^2-8=0\)
hay \(x\in\left\{2\sqrt{2};-2\sqrt{2}\right\}\)

a: Ta có: \(x^2+3x+4=0\)
\(\text{Δ}=3^2-4\cdot1\cdot4=9-16=-7< 0\)
Do đó: Phương trình vô nghiệm

`1)(x+2)(x+3)(x-7)(x-8)=144`
`<=>[(x+2)(x-7)][(x+3)(x-8)]=144`
`<=>(x^2-5x-14)(x^2-5x-24)=144`
`<=>(x^2-5x-19)^2-25=144`
`<=>(x^2-5x-19)^2-169=0`
`<=>(x^2-5x-6)(x^2-5x-32)=0`
`+)x^2-5x-6=0`
`<=>` $\left[ \begin{array}{l}x=6\\x=-1\end{array} \right.$
`+)x^2-5x-32=0`
`<=>` $\left[ \begin{array}{l}x=\dfrac{5+3\sqrt{17}}{2}\\x=\dfrac{5-3\sqrt{17}}{2}\end{array} \right.$
Vậy `S={-1,6,\frac{5+3\sqrt{17}}{2},\frac{5-3\sqrt{17}}{2}}`
1: Ta có: \(\left(x+2\right)\left(x+3\right)\left(x-7\right)\left(x-8\right)=144\)
\(\Leftrightarrow\left(x^2-7x+2x-14\right)\left(x^2-8x+3x-24\right)=144\)
\(\Leftrightarrow\left(x^2-5x-14\right)\left(x^2-5x-24\right)-144=0\)
\(\Leftrightarrow\left(x^2-5x\right)^2-38\left(x^2-5x\right)+336-144=0\)
\(\Leftrightarrow\left(x^2-5x\right)^2-38\left(x^2-5x\right)+192=0\)
\(\Leftrightarrow\left(x^2-5x\right)^2-6\left(x^2-5x\right)-32\left(x^2-5x\right)+192=0\)
\(\Leftrightarrow\left(x^2-5x\right)\left(x^2-5x-6\right)-32\left(x^2-5x-6\right)=0\)
\(\Leftrightarrow\left(x^2-5x-6\right)\left(x^2-5x-32\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+1\right)\left(x^2-5x-32\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x+1=0\\x^2-5x-32=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-1\\x=\dfrac{5-3\sqrt{17}}{2}\\x=\dfrac{5+3\sqrt{17}}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{6;-1;\dfrac{5-3\sqrt{17}}{2};\dfrac{5+3\sqrt{17}}{2}\right\}\)

\(x^4-9x^2+24x-16=\)\(0\)
\(\Leftrightarrow x^4-\left(9x^2-24x+16\right)=0\)
\(\Leftrightarrow x^4-\left(3x-4\right)^2=0\)
\(\Leftrightarrow\left(x^2+3x-4\right)\left(x^2-3x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-1\right)\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]=0\)
Vì \(\left(x-\frac{3}{2}\right)^2+\frac{7}{4}>0\forall x\)nên:
\(\left(x+4\right)\left(x-1\right)=0:\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]\)
\(\Leftrightarrow\left(x+4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\x-1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=1\end{cases}}\)
Vậy phương trình có tập nghiệm \(S=\left\{1;-4\right\}\)
\(x^4=6x^2+12x+\)\(8\)
\(\Leftrightarrow x^4-2x^2+1=4x^2+12x+9\)
\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)
\(\Leftrightarrow|x^2-1|=|2x+3|\)\(|\)
xét các trường hợp:
- Trường hợp 1:
\(x^2-1=2x+3\)
\(\Leftrightarrow x^2-1-2x-3=0\)
\(\Leftrightarrow x^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2-5=0\Leftrightarrow\left(x-1\right)^2=5\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=\sqrt{5}\\x-1=-\sqrt{5}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1+\sqrt{5}\\x=1-\sqrt{5}\end{cases}}}\)
-Trường hợp 2:
\(x^2-1=-2x-3\)
\(\Leftrightarrow x^2-1+2x+3=0\)
\(\Leftrightarrow x^2+2x+2=0\)
\(\Leftrightarrow\left(x+1\right)^2+1=0\)
\(\Leftrightarrow\left(x+1\right)^2=-1\left(vn\right)\)(vô nghiệm)
Vậy phương trình có tập nghiệm: \(S=\left\{1\pm\sqrt{5}\right\}\)

\(ĐK:x\ge-3\\ PT\Leftrightarrow x^2-x+8-4\sqrt{x+3}=0\\ \Leftrightarrow x\left(x-1\right)-4\left(\sqrt{x+3}-2\right)=0\\ \Leftrightarrow x\left(x-1\right)-\dfrac{4\left(x-1\right)}{\sqrt{x+3}+2}=0\\ \Leftrightarrow\left(x-1\right)\left(x-\dfrac{4}{\sqrt{x+3}+2}\right)=0\\ \Leftrightarrow x=1\left(x-\dfrac{4}{\sqrt{x+3}+2}< 0\right)\)

\(pt\Leftrightarrow\left[\left(x-4\right)\left(x-10\right)\right]\left[\left(x-5\right)\left(x-8\right)\right]=72x^2\)
\(\Leftrightarrow\left(x^2+40-14x\right)\left(x^2+40-13x\right)=72x^2\)
\(x=0\) không phải là nghiệm của phương trình trên
Xét \(x\ne0\)
\(pt\Leftrightarrow\frac{x^2+40-14x}{x}.\frac{x^2+40-13x}{x}=72\)
\(\Leftrightarrow\left(x+\frac{40}{x}-14\right)\left(x+\frac{40}{x}-13\right)=72\)
Đặt \(x+\frac{40}{x}-14=a\)
\(pt\rightarrow a\left(a+1\right)=72\Leftrightarrow a^2+a-72=0\Leftrightarrow\orbr{\begin{cases}a=8\\a=-9\end{cases}}\)
TH1: a = 8 \(\Rightarrow x+\frac{40}{x}-14=8\Leftrightarrow\frac{x^2-22x+40}{x}=0\Leftrightarrow\orbr{\begin{cases}x=2\\x=20\end{cases}}\)
TH2: a = -9 \(\Rightarrow x+\frac{40}{x}-14=-9\Leftrightarrow\frac{x^2-5x+40}{x}=0\text{ }\left(\text{vô nghiệm }\right)\)

\((x+1)(x+2)(x+4)(x+8)=28x^2\)
\(\Leftrightarrow\text{(x}^2+6\text{x}+8)(\text{x}^2+9\text{x}+8)=28\text{x}^2\) \((1)\)
Thấy x = 0 không là nghiệm của \((1)\). Chia \((2)\)vế \((1)\)cho \(\text{x}^2\)ta được :
\((1)\Leftrightarrow(\text{x}+\frac{8}{\text{x}}+6)(\text{x}+\frac{8}{9}+9)=28\)
Đặt \(\text{t}=\text{x}+\frac{8}{\text{x}}\). Ta có :
\((1)\Leftrightarrow(\text{t}+6)(\text{t}+9)=28\)
\(\Leftrightarrow\text{t}^2+15\text{t}+26=0\Leftrightarrow\orbr{\begin{cases}\text{t}=-2\\\text{t}=-13\end{cases}}\)
- Với \(\text{t}=-2\)\(\Rightarrow\text{x}+\frac{8}{\text{x}}=-2\Leftrightarrow\text{x}^2+2\text{x}+8=0\Leftrightarrow(\text{x}+1)^2+7>0\)\((\)vô nghiệm\()\)
- Với \(t=-13\Rightarrow x+\frac{8}{x}=-13\Leftrightarrow x^2+13x+8=0\)
\(\Delta=13^2-4(1\cdot8)=137\Rightarrow x_{1,2}=\frac{-13\pm\sqrt{137}}{2}\)\((\)thỏa mãn\()\)
Vậy :
TL bạn cho mình hỏi là ở chỗ chia 2 về (1) cho \(x^2\) sao lại ra cái phần dưới vậy

\(\sqrt{24+8\sqrt{9-x^2}}=x+2\sqrt{3-x}+4\) \(\left(Đk:-3\le x\le3\right)\)
\(\sqrt{4\left(x+3\right)+8\sqrt{9-x^2}+4\left(3-x\right)}=x+2\sqrt{3-x}+4\)
\(\sqrt{\left(2\sqrt{x+3}+2\sqrt{3-x}\right)^2}=x+2\sqrt{3-x}+4\)
\(2\sqrt{x+3}+2\sqrt{3-x}=x+2\sqrt{3-x}+4\)
\(2\sqrt{x+3}=x+4\)
\(4\left(x+3\right)=x^2+8x+14\)
\(x^2+4x+2=0\)
\(\Delta=16-8=8\)
\(\Delta>0\)=> phương trình có 2 nghiệm phân biệt
\(\left[{}\begin{matrix}x=\dfrac{-4+2\sqrt{2}}{2}=-2+\sqrt{2}\\x=\dfrac{-4-2\sqrt{2}}{2}=-2-\sqrt{2}\end{matrix}\right.\)

\(\left(x-8\right)\left(x-4\right)\left(x-2\right)\left(x-1\right)=270x^2\)
\(\Rightarrow\left(x-8\right)\left(x-1\right)\left(x-4\right)\left(x-2\right)-270x^2=0\)
\(\Rightarrow\left(x^2-9x+8\right)\left(x^2-6x+8\right)-270x^2=0\)
Đặt \(x^2-6x+8=t\), ta có phương trình mới: \(\left(t-3x\right)t-270x^2=0\)
\(\Leftrightarrow t^2-3xt-270x^2=0\)
Với x = 0, t = 8, phương trình không thỏa mãn. Vậy \(x\ne0\)
Chia cả hai vế cho x2, ta có: \(\left(\frac{t}{x}\right)^2-3\left(\frac{t}{x}\right)-270=0\)
\(\Leftrightarrow\orbr{\begin{cases}\frac{t}{x}=18\\\frac{t}{x}=-15\end{cases}}\)
Với \(\frac{t}{x}=18\Rightarrow x^2-6x+8=18x\Rightarrow x^2-24x+8=0\Rightarrow x=12\pm2\sqrt{34}\)
Với \(\frac{t}{x}=-15\Rightarrow x^2-6x+8=-15x\Rightarrow x^2+9x+8=0\Rightarrow\orbr{\begin{cases}x=-1\\x=-8\end{cases}}\)
Vậy phương trình có 4 nghiệm \(S=\left\{-8;-1;12-2\sqrt{34};12+2\sqrt{34}\right\}\)

ĐK: `x^2-4x+4>=0<=>(x-2)^2>=0 forall x`
`\sqrt(x^2-4x+4)+x=8`
`<=>\sqrt((x-2)^2)+x=8`
`<=>|x-2|+x=8`
`<=> [(x-2+x=8),(-x+2+x=8):}`
`<=>[(x=5),(VN):}`
Vậy `x=5`
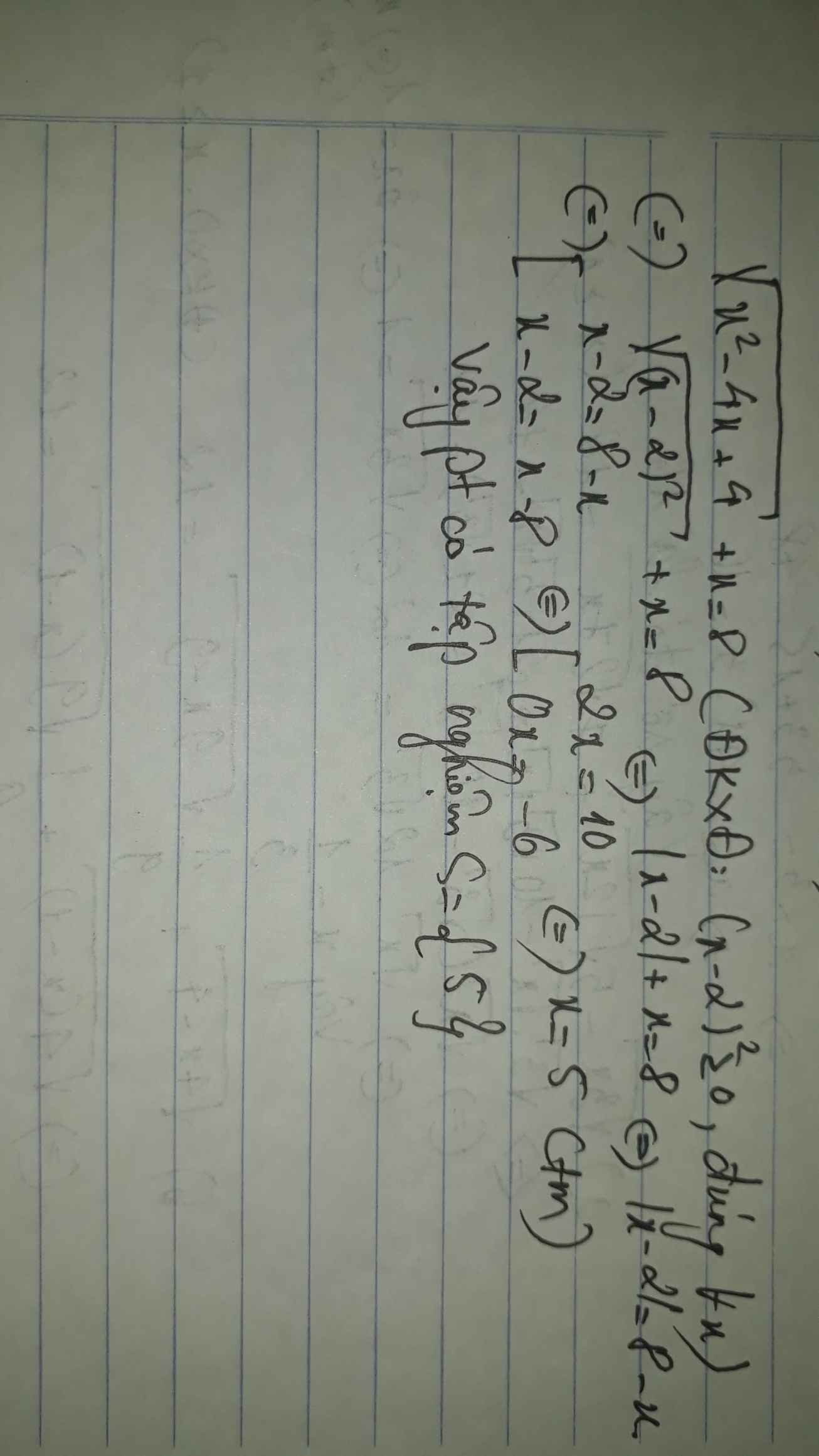
Điều kiện : x ≠ 2 và x ≠ -4
Ta có: 2 x x - 2 - x x + 4 = 8 x + 8 x - 2 x + 4 ⇔ 2x(x +4) –x(x -2) = 8x +8
⇔ 2 x 2 +8x – x 2 +2x = 8x +8
⇔ x 2 +2x -8 = 0
∆ ’ = 1 2 -1(-8) = 1 +8 = 9 > 0
∆ ' = 9 = 3
Cả hai giá trị của x đều không thỏa mãn điều kiện bài toán
Vậy phương trình đã cho vô nghiệm