K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 11 2021
Bài 3:
Diện tích là:
\(15\cdot6=90\left(m^2\right)\)
13 tháng 11 2021
Bài 3:
Gọi cd,cr lần lượt là a,b(m;a,b>0)
Áp dụng tc dtsbn:
\(\dfrac{b}{a}=\dfrac{2}{5}\Rightarrow\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a+2b}{10+4}=\dfrac{42}{14}=3\\ \Rightarrow\left\{{}\begin{matrix}a=15\\b=6\end{matrix}\right.\\ \Rightarrow S_{hcn}=ab=90\left(m^2\right)\)
Bài 4:
Gọi cd,cr lân lượt là a,b(m;a,b>0)
Đặt \(\dfrac{a}{4}=\dfrac{b}{3}=k\Rightarrow a=4k;b=3k\)
\(ab=300\left(m^2\right)\\ \Rightarrow12k^2=300\\ \Rightarrow k^2=25\Rightarrow k=5\left(k>0\right)\\ \Rightarrow\left\{{}\begin{matrix}a=20\\b=15\end{matrix}\right.\)
Vậy ...
Bài 5:
Gọi số hs 7A,7B,7C,7D ll là a,b,c,d(hs;a,b,c,d∈N*)
Áp dụng tc dtsbn:
\(\dfrac{a}{11}=\dfrac{b}{12}=\dfrac{c}{13}=\dfrac{d}{14}=\dfrac{2b-a}{24-11}=\dfrac{39}{13}=3\\ \Rightarrow\left\{{}\begin{matrix}a=33\\b=36\\c=39\\d=42\end{matrix}\right.\)
Vậy ...
NT
6 tháng 9 2021
c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
KK
6 tháng 9 2021
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)
DT
3
6 tháng 9 2021
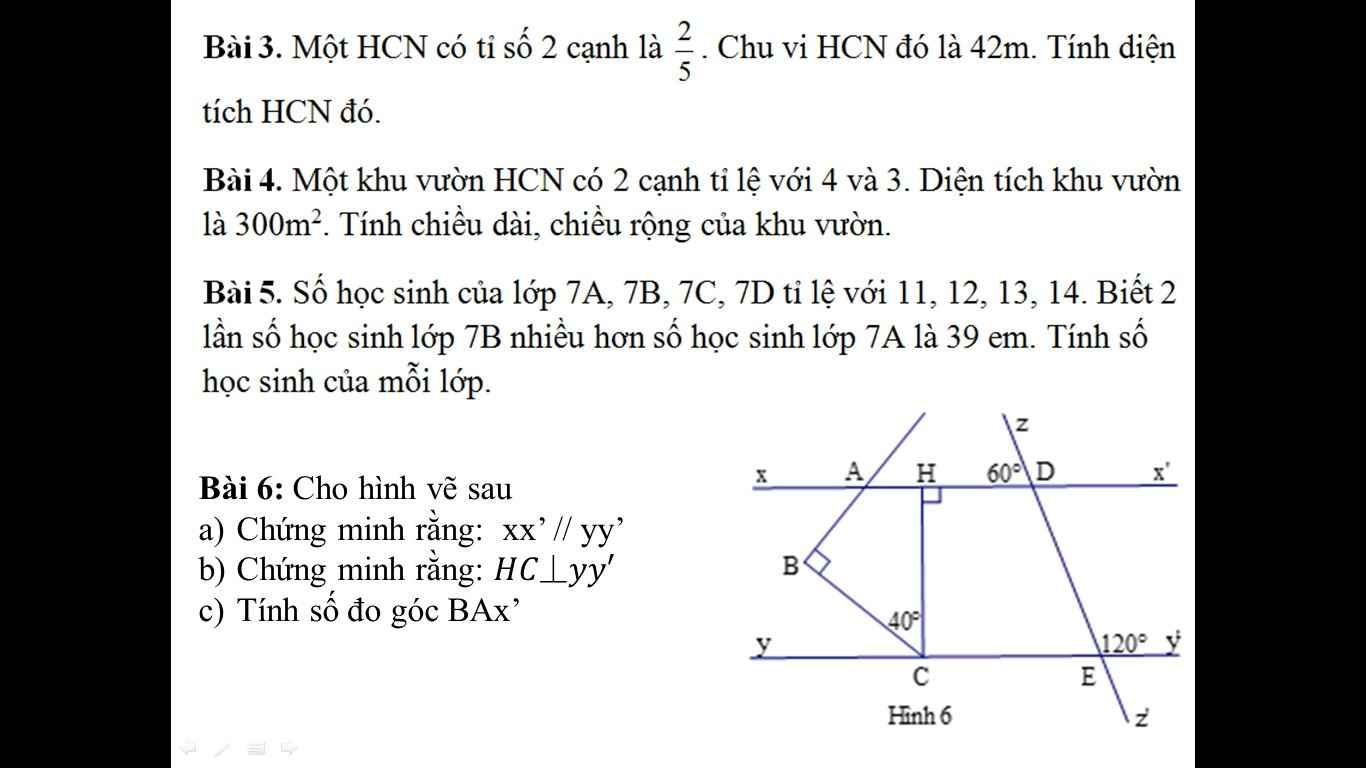
Ta có : a song song với b
=> Góc A = Góc B = 90độ
Hay x = 90 độ
=> Góc D + Góc C = 180độ ( 2 góc trong cùng phía )
=> y + 130 độ = 180 độ
=> y = 50 độ
6 tháng 9 2021
Vẽ Cx song song với Am(1), ta được :
=> Góc mAC + Góc ACx = 180 độ
=> Góc mAC + Góc BCA + Góc BCx = 180 độ
Hay Góc BCx = 180 độ - 45 độ - 60 độ = 75 độ
Vì Góc nBC + Góc BCx = 180 độ ( 75 độ + 105 độ = 180 độ )
Mà Góc nBC và Góc BCx là 2 góc trong cùng phía
Nên ta được Bn song song với Cx (2)
Từ (1) và (2) => Bn song song với Am
24 tháng 10 2021
27: \(\sqrt{\dfrac{81}{25}}-\dfrac{1}{5}\left(-3+\sqrt{16}\right)^{20}\cdot\left(-2\right)^3\)
\(=\dfrac{9}{5}-\dfrac{1}{5}\cdot\left(-8\right)\)
\(=\dfrac{9}{5}+\dfrac{8}{5}=\dfrac{17}{5}\)
28: \(\sqrt{\sqrt{16}}-\sqrt{\sqrt{81}}=2-3=-1\)
5 tháng 1 2022
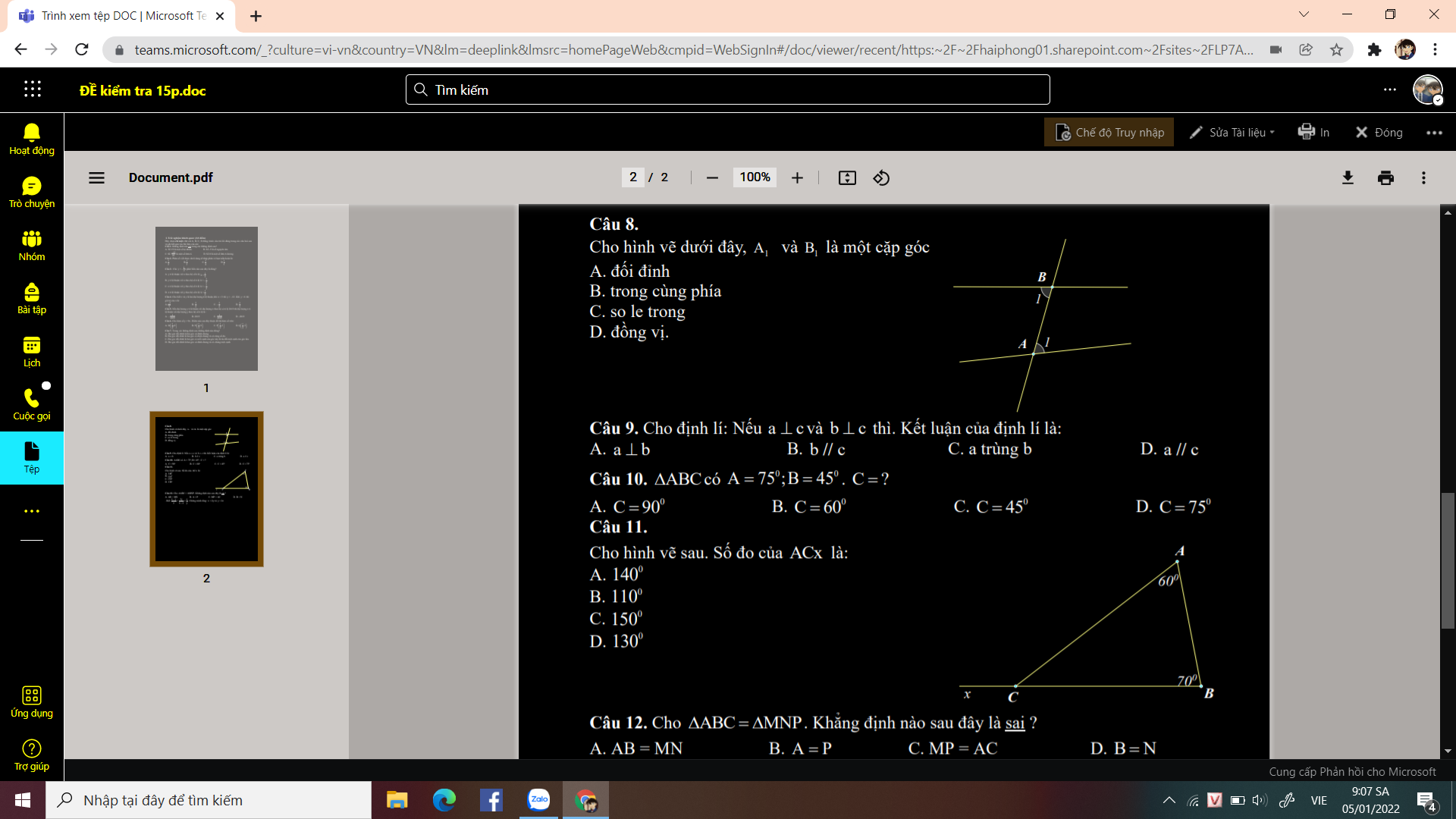
\(\text{8.C.So le trong}\)
\(\text{9.C.a trùng b}\)
\(\text{10.B.}60^0\)
\(\text{11.C.}150^0\)
\(\text{12.B.A=P}\)
2 tháng 3 2020
\(2^x:1+2^x:2+...+2^x:49=2^{49}-1\)
\(2^x.1+2^x.\frac{1}{2}+...+2^x.\frac{1}{49}=2^{49}-1\)
\(2^x.\left(1+\frac{1}{2}+...+\frac{1}{49}\right)=2^{49}-1\)
3 tháng 3 2020
Đặt: \(A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{49}}\)
=> \(2A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{48}}\)
=> \(2A-A=\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{48}}\right)-\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^{49}}\right)\)
=> \(A=1-\frac{1}{2^{49}}=\frac{2^{49}-1}{2^{49}}\)
\(2^{x-1}+2^{x-2}+2^{x-3}+...+2^{x-49}=2^{49}-1\)
<=> \(\frac{2^x}{2}+\frac{2^x}{2^2}+\frac{2^x}{2^3}+...+\frac{2^x}{2^{49}}=2^{49}-1\)
<=> \(2^x\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{49}}\right)=2^{49}-1\)
<=> \(2^x.\frac{2^{49}-1}{2^{49}}=2^{49}-1\)
<=> \(2^x=2^{49}\)
<=> x = 49.
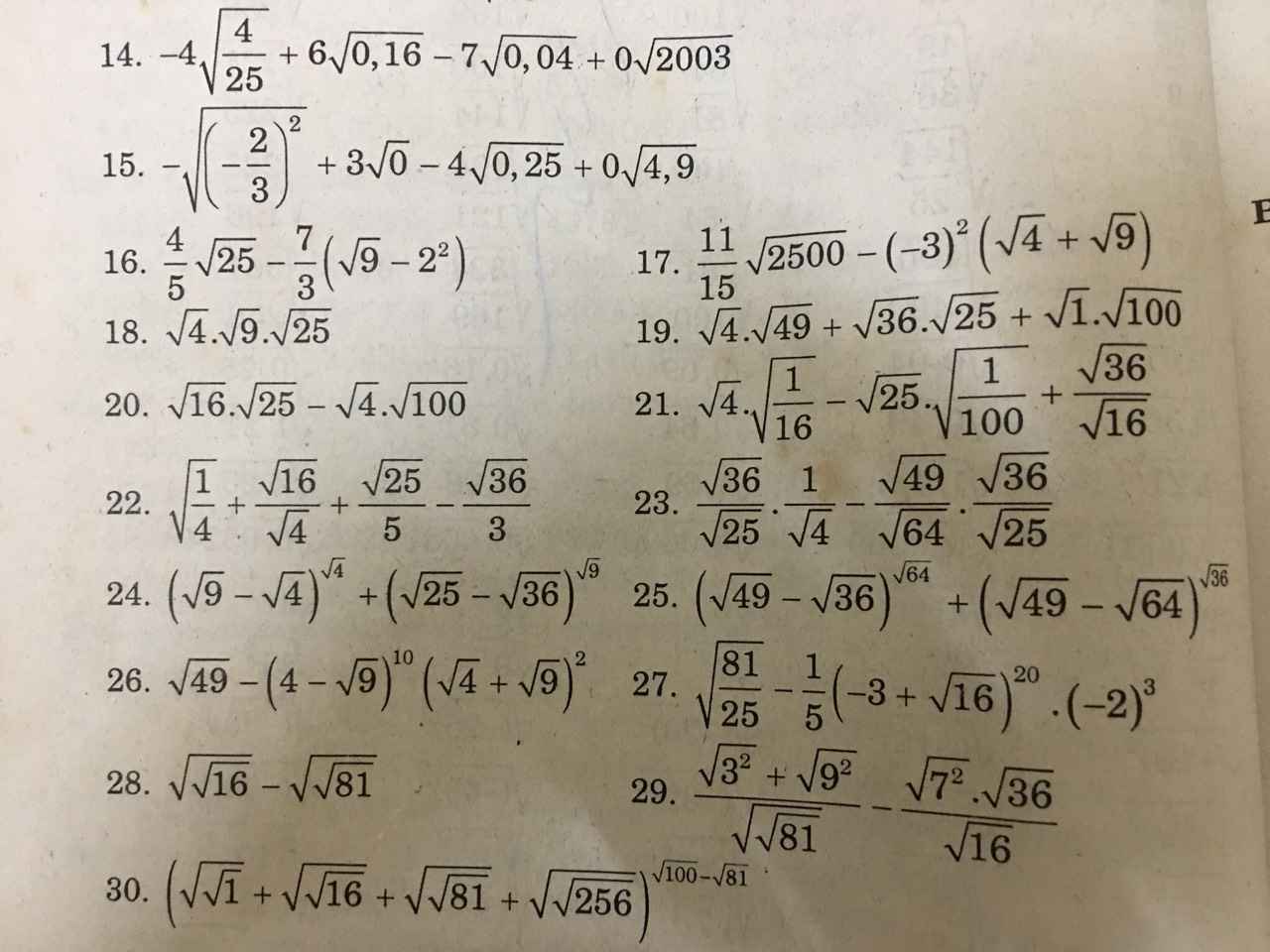
Câu 3:
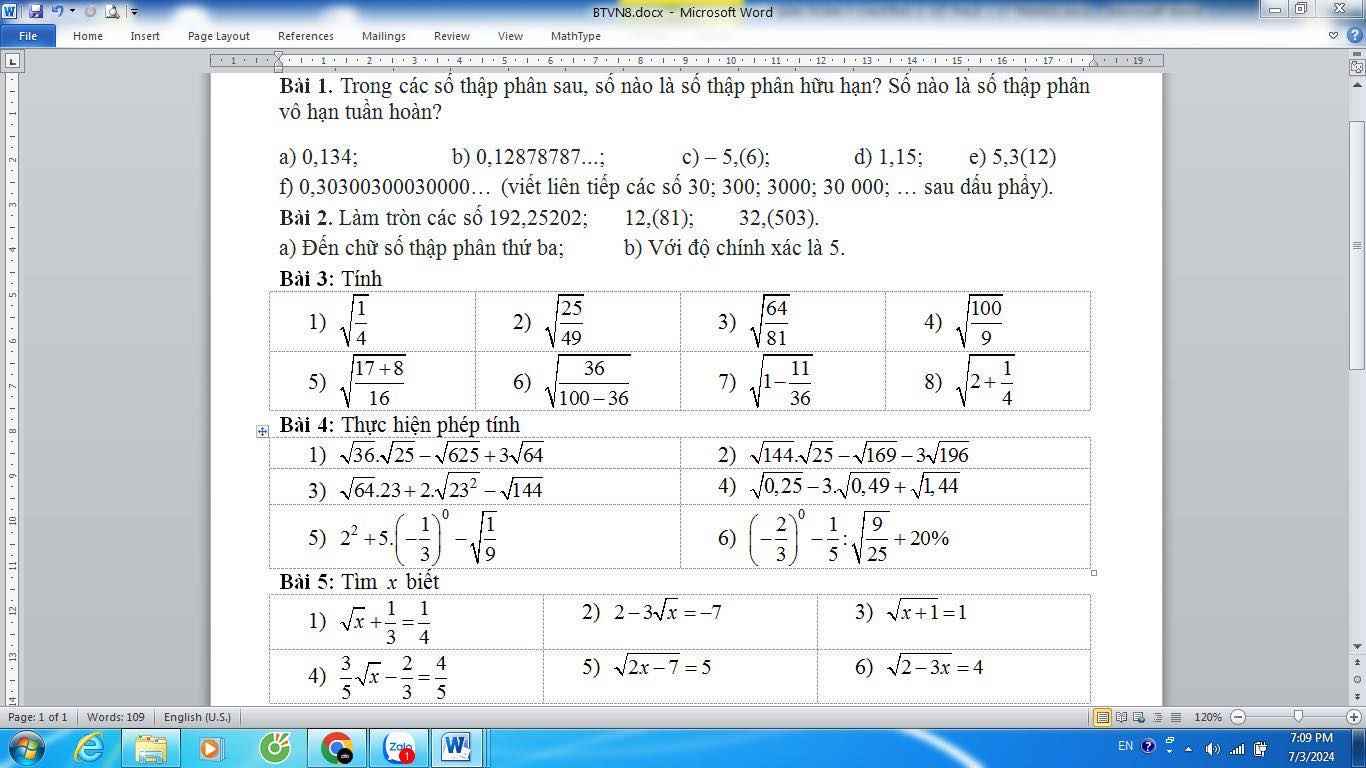
1: \(\sqrt{\dfrac{1}{4}}=\dfrac{\sqrt{1}}{\sqrt{4}}=\dfrac{1}{2}\)
2: \(\sqrt{\dfrac{25}{49}}=\dfrac{\sqrt{25}}{\sqrt{49}}=\dfrac{5}{7}\)
3: \(\sqrt{\dfrac{64}{81}}=\dfrac{\sqrt{64}}{\sqrt{81}}=\dfrac{8}{9}\)
4: \(\sqrt{\dfrac{100}{9}}=\dfrac{\sqrt{100}}{\sqrt{9}}=\dfrac{10}{3}\)
5: \(\sqrt{\dfrac{17+8}{16}}=\sqrt{\dfrac{25}{16}}=\dfrac{\sqrt{25}}{\sqrt{16}}=\dfrac{5}{4}\)
6: \(\sqrt{\dfrac{36}{100-36}}=\sqrt{\dfrac{36}{64}}=\sqrt{\dfrac{9}{16}}=\dfrac{\sqrt{9}}{\sqrt{16}}=\dfrac{3}{4}\)
7: \(\sqrt{1-\dfrac{11}{36}}=\sqrt{\dfrac{36}{36}-\dfrac{11}{36}}=\sqrt{\dfrac{25}{36}}=\dfrac{\sqrt{25}}{\sqrt{36}}=\dfrac{5}{6}\)
8: \(\sqrt{2+\dfrac{1}{4}}=\sqrt{\dfrac{9}{4}}=\dfrac{\sqrt{9}}{\sqrt{4}}=\dfrac{3}{2}\)
Câu 5:
1: ĐKXĐ: x>=0
\(\sqrt{x}+\dfrac{1}{3}=\dfrac{1}{4}\)
=>\(\sqrt{x}=\dfrac{1}{4}-\dfrac{1}{3}=-\dfrac{1}{12}\)<0(vô lý)
=>Phương trình vô nghiệm
2: ĐKXĐ: x>=0
\(2-3\sqrt{x}=-7\)
=>\(3\sqrt{x}=2+7=9\)
=>\(\sqrt{x}=3\)
=>\(x=3^2=9\)(nhận)
3: ĐKXĐ: x+1>=0
=>x>=-1
\(\sqrt{x+1}=1\)
=>\(x+1=1^2=1\)
=>x=1-1=0(nhận)
4: ĐKXĐ: x>=0
\(\dfrac{3}{5}\sqrt{x}-\dfrac{2}{3}=\dfrac{4}{5}\)
=>\(\dfrac{3}{5}\sqrt{x}=\dfrac{2}{3}+\dfrac{4}{5}=\dfrac{10}{15}+\dfrac{12}{15}=\dfrac{22}{15}\)
=>\(\sqrt{x}=\dfrac{22}{15}:\dfrac{3}{5}=\dfrac{22}{15}\cdot\dfrac{5}{3}=\dfrac{110}{45}=\dfrac{22}{9}\)
=>\(x=\left(\dfrac{22}{9}\right)^2=\dfrac{264}{81}\)
5: ĐKXĐ: 2x-7>=0
=>x>=7/2
\(\sqrt{2x-7}=5\)
=>\(2x-7=5^2=25\)
=>2x=7+25=32
=>x=32/2=16(nhận)
6: ĐKXĐ: 2-3x>=0
=>3x<=2
=>\(x< =\dfrac{2}{3}\)
\(\sqrt{2-3x}=4\)
=>\(2-3x=4^2=16\)
=>3x=2-16=-14
=>\(x=-\dfrac{14}{3}\left(nhận\right)\)