Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đường thẳng d: y = mx + n và parabol (P): y = a x 2 cắt nhau tại hai điểm phân biệt khi phương trình a x 2 = m . x + n có hai nghiệm phân biệt.
Đáp án: A
\(mx^2+2\left(m-1\right)x+m+3=0\)(Đk:m≠0)
\(\Delta'=\left(m-1\right)^2-m\left(m+3\right)\)
\(\Delta'=m^2-2m+1-m^2-3m\)
\(\Delta'=1-5m\)
a,Để pt có nghiệm kép
Thì\(\Delta'=0\)
\(\Leftrightarrow1-5m=0\Rightarrow m=\dfrac{1}{5}\)
b, Để pt có 2 nghiệm phân biệt
Thì\(\Delta'>0\)
\(\Leftrightarrow1-5m>0\Rightarrow m< \dfrac{1}{5}\)
c,Để pt có nghiệm
Thì\(\Delta'\ge0\)
\(\Leftrightarrow1-5m\ge0\Rightarrow m\le\dfrac{1}{5}\)
d, Để pt vô nghiệm
Thì\(\Delta'< 0\)
\(\Leftrightarrow1-5m< 0\Rightarrow m>\dfrac{1}{5}\)
Lời giải:
$m=0$ thì pt trở thành $-2x+3=0\Leftrightarrow x=\frac{3}{2}$
$m\neq 0$ thì pt là pt bậc 2 ẩn $x$
$\Delta'=(m-1)^2-m(m+3)=1-5m$
PT có nghiệm kép $\Leftrightarrow \Delta'=1-5m=0\Leftrightarrow m=\frac{1}{5}$
PT có 2 nghiệm pb $\Leftrightarrow \Delta'=1-5m>0$
$\Leftrightarrow m< \frac{1}{5}$
Vậy pt có 2 nghiệm pb khi $m< \frac{1}{5}$ và $m\neq 0$
PT có nghiệm khi \(\left[\begin{matrix} m=0\\ \Delta'=1-5m\geq 0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} m=0\\ m\leq \frac{1}{5}\end{matrix}\right.\Leftrightarrow m\leq \frac{1}{5}\)
PT vô nghiệm khi $\Delta'=1-5m< 0$
$\Leftrightarrow m> \frac{1}{5}$
Đường thẳng d: y = mx + n và parabol (P): y = a x 2 không cắt nhau khi phương trình a x 2 = m . x + n vô nghiệm
Đáp án: C
a, Để pt có 2 nghiệm pb khi \(\Delta>0\)
\(\Delta=\left(-2m\right)^2-4\left(m+6\right)=4m^2-4m-24>0\Leftrightarrow m< -2;m>3\)
b, Để pt trên là pt bậc 2 khi \(m\ne0\)
Để pt vô nghiệm khi \(\Delta< 0\)
\(\Delta=4m^2-4m\left(m+3\right)=4m^2-4m^2-12m< 0\Leftrightarrow-12m< 0\Leftrightarrow m>0\)
c, Để pt trên là pt bậc 2 khi \(m\ne2\)
Để pt trên có nghiệm kép \(\Delta=0\)
\(\Delta=\left(2m-3\right)^2-4\left(m+1\right)\left(m-2\right)=4m^2-12m+9-4\left(m^2-m-2\right)\)
\(=-8m+17=0\Leftrightarrow m=\frac{17}{8}\)
a) Phương trình x 2 – 2 ( m – 1 ) x + m 2 = 0 (1)
Có a = 1; b’ = -(m – 1); c = m 2
b) Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m >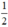 
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =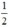 
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <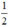 
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m <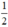 
; có nghiệm kép khi m = 
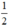và vô nghiệm khi m >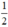 
a)(m-1)x2+2(m-1)x-m
pt bậc 2 có dạng ax2+bx+c=0.
a=(m-1);b=(m-1);c=-m
áp dụng b2-4ac.ta có:Denta=(m-1)2-4[(-m)*(m-1)]
Để pt có nghịm kép =>Denta=0
=>(m-1)2-4[(-m)*(m-1)]=0
=>m=1 hoặc m=0
Thay với m=1 vào và m=0 vào tự tính
b)Để pt có 2 nghiệm phân biệt thì Denta>0
=>(m-1)2-4[(-m)*(m-1)]>0
=>5m2-6m+1>0
Giải BPT này ra
à mk thêm 1 bước nữa để bạn giải cho nhẹ
5m2-6m+1>0
<=>(m-1)(5m-1)>0 tới đây học sinh lớp 6 cx có thể giải đc nhé chúc bạn học tốt
a: Δ=(4m+3)^2-4*2*(2m^2-1)
=16m^2+24m+9-16m^2+8
=24m+17
Để phương trình có hai nghiệm phân biệt thì 24m+17>0
=>m>-17/24
b: Để phương trìh có nghiệm kép thì 24m+17=0
=>m=-17/24
c: Để phương trình vô nghiệm thì 24m+17<0
=>m<-17/24
Đường thẳng d và parabol (P) tiếp xúc với nhau khi phương trình a. x 2 = m.x + n ↔a. x 2 − m.x – n = 0 vô nghiệm (∆< 0)
Đáp án: C