Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hình bình hành \(ABCD\)có \(O\)là giao điểm của \(AC\)và \(BD\).
Khi đó \(O\)là trung điểm của \(AC\)và \(BD\).
Độ dài hai đường chéo tỉ lệ với độ dài hai cạnh liên tiếp nên \(\frac{BD}{AC}=\frac{AB}{AD}\Leftrightarrow\frac{DA}{OA}=\frac{AB}{OB}\).
Xét tam giác \(DAB\)và tam giác \(AOB\)có:
\(\widehat{DBA}=\widehat{ABO}\)(góc chung)
\(\frac{DA}{AO}=\frac{AB}{OB}\)(cmt)
Suy ra \(\Delta DAB~\Delta AOB\left(c.g.c\right)\).
suy ra \(\widehat{AOB}=\widehat{DAB}\)(hai góc tương ứng)
Ta có đpcm.

A) Vẽ t/g ABC (A là góc nhọn), đường cao BH.
1/2.AB.AC.sinA = 1/2.AB.AC.(BH/AB) = 1/2.BH.AC = S(ABC)

Gọi hình bình hành đó là ABCD , từ A kẻ đường cao AH xuống cạnh CD (H thuộc CD)
Ta có : \(AH=AD.sinD\)
\(\Rightarrow S_{ABCD}=CD.AH=CD.AD.sinD\)
Vậy ta có điều phải chứng minh

bạn giải ra bài này chưa mình đang luyện thi casio nếu bạn biết hãy chỉ giúp mình nhá

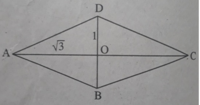
Coi đường chéo AC = 2 3 , đường chéo BD = 2 thì để ý rằng AC và BD vuông góc, ta có
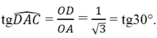
Nên ∠ (DAC) = 30 ° từ đó góc A của hình thoi là 60 ° . Suy ra ∠ C = 60 ° còn ∠ B = ∠ D = 120 °

Lời giải:
Xét tam giác vuông $ABC$ có:
$\frac{AC}{BC}=\sin \widehat{ABC}$
$\Leftrightarrow \frac{AC}{12}=\sin 60^0$
$\Rightarrow AC=12.\sin 60^0=6\sqrt{3}$ (m)