NM
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 4 2023
Gọi điểm thi tuyển sinh là x
=>Điểm thi lần 2 là: 0,8x
ĐIểm thi lần 1 là: 0,8x*2/3=8/15x
Theo đề, ta có: x=1/2(0,8x+8/15x)+2,5
=>x=0,4x+4/15x+2,5
=>2/3x+2,5=x
=>-1/3x=-2,5
=>x=7,5
T
1
VL
3
12 tháng 6 2021
câu: 7:
pt hoành độ giao điểm : \(x^2=3x+m< =>x^2-3x-m=0\)
\(\Delta=\left(-3\right)^2-4\left(-m\right)=9+4m\)
để (P) và(d) không có điểm chung\(< =>9+4m< 0< =>m< \dfrac{-9}{4}\)
Vậy ....
S
12 tháng 6 2021
Câu 6
Áp dụng hệ thức: \(\sin^2\alpha+\cos^2\alpha=1\Rightarrow\cos^2\alpha=1-\sin^2\alpha\)
\(\Rightarrow\cos^2\alpha=1-0,6^2=0,64\)
\(\Rightarrow\cos\alpha=\pm0,8\)
Mà \(\alpha\) là góc nhọn nên \(\cos\alpha>0\) do đó \(\cos\alpha=0,8\)
Ta có: \(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{0,6}{0,8}=0,75\)
Khi đó \(B=5\cos\alpha-4\tan\alpha=5.0,8-4.0,75=1\)
21 tháng 3 2021
Gọi vận tốc dự định của ô tô là x ( km/h ; x > 0 )
=> Thời gian ô tô dự kiến đến B = 90/x ( giờ )
Thực tế vận tốc của ô tô = x+5 (km/h)
Khi đó thời gian ô tô đến B trên thực tế = 90/x+5 + 1/5 ( giờ )
Theo bài ra ta có phương trình : \(\frac{90}{x}=\frac{90}{x+5}+\frac{1}{5}\)
<=> \(\frac{1}{x}-\frac{1}{x+5}=\frac{1}{450}\)<=> \(\frac{5}{x\left(x+5\right)}=\frac{1}{450}\)
=> 2250 = x2 + 5x
<=> x2 + 5x - 2250 = 0
Δ = b2 - 4ac = (5)2 - 4.(-2250) = 9025
Δ > 0, áp dụng công thức nghiệm thu được x1 = 45 (tm) ; x2 = -50 (ktm)
Vậy ...
21 tháng 3 2021
Gọi độ dài của mỗi cạnh của hình chữ nhật là x, và y (m)
Đk : x, y > 0
Tổng độ dài 2 cạnh là:
x + y = 24/2
=> x + y = 12 (1)
Nếu tăng độ dài 1 cạnh (x) lên 2m và giảm cạnh còn lại (y) 1m thì diện tích mảnh đất tăng thêm 1m², ta có:
(x + 2).(y - 1) = xy + 1
=> xy - x + 2y - 2 = xy + 1
=> 2y - x = 3 (2)
Từ (1) và (2), ta có hệ phương trình:
{ x + y = 12
2y - x = 3
=> { x = 12 - y
2y - x + x + y = 3 + 12
=> { x = 12 - y
3y = 15
=> { x = 7 (tm)
y = 5 (tm)
Vậy độ dài các cạnh của hình chữ nhật là 7m và 5m.
DQ
16
11 tháng 6 2021
Bài 5
\(a - b = 2 <=> b = a - 2\)
Do đó: \(P = 3a^2 + (a-2)^2 + 8\)
\(= 3a^2 + a^2 - 4a + 4 + 8\)
\(= 4a^2 - 4a + 12\)
\(= (2a - 1)^2 + 11\)
Vì \((2a - 1)^2 \geq 0 \) với mọi a nên \(= (2a - 1)^2 + 11 \geq 11 \) hay \(P \geq 11\)
Dấu "=" xảy ra \(\begin{cases} a - b = 2 \\ 2a - 1 = 0 \\\end{cases} <=> \begin{cases} a = \dfrac{1}{2} \\ b = -\dfrac{3}{2} \\\end{cases}\)
Vậy giá trị nhỏ nhất của P là 11 tại \(\begin{cases} a = \dfrac{1}{2} \\ b = -\dfrac{3}{2} \\\end{cases}\)
AT
11 tháng 6 2021
câu hình:
a) Vì AB là đường kính \(\Rightarrow\angle ADB=90\Rightarrow\angle EDB+\angle EHB=180\)
\(\Rightarrow EDHB\) nội tiếp
b) Xét \(\Delta AHE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle DABchung\\\angle AHE=\angle ADB=90\end{matrix}\right.\)
\(\Rightarrow\Delta AHE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AH}{AD}=\dfrac{AE}{AB}\Rightarrow AB.AH=AD.AE\)
mà \(AH.AB=AC^2\) (hệ thức lượng) \(\Rightarrow AC^2=AD.AE\)
c) Vì \(EF\parallel AB\) \(\Rightarrow\angle CFE=\angle CBA=\angle CDA=\angle CDE\)
\(\Rightarrow CDFE\) nội tiếp mà \(\angle CEF=90\) \((EF\parallel AB,AB\bot CH)\)
\(\Rightarrow\angle CDF=90\Rightarrow CD\bot DF\)
Vì \(\Delta CDF\) vuông tại D có K là trung điểm CF \(\Rightarrow KC=KD\)
\(\Rightarrow\Delta KCD\) cân tại K \(\Rightarrow\angle DKB=2\angle DCB=2\angle DAB=\angle DOB\)
\(\Rightarrow DKOB\) nội tiếp \(\Rightarrow K\in\left(OBD\right)\)
21 tháng 3 2021
Gọi số cây mỗi HS dự định trồng là x (cây). Đk: x > 0, x nguyên.
Số Hs là em
Số cây thực tế mỗi em trồng là x + 5 cây
Số Hs thực tế là:
Theo bài ra ta có pt:
- = 2
Giải pt ta được x = - 25 (loại) và x = 20 (nhận)
Vậy số HS thực tế đã tham gia là: = 8 em
TA
8 tháng 6 2021
Câu 1
a) `\sqrt64+\sqrt16-2\sqrt36`
`=\sqrt(8^2)+\sqrt(4^2) - 2\sqrt(6^2)`
`=8+4-12=0`
b) `y=ax+b //// y=3x => a=3`
`=> y=3x+b`
`M(1;9) \in y=3x+b <=> 9=3.1+b <=> b=6`
`=> y=3x+6`
c) `P=(1/(\sqrtx) - 2/(1+\sqrtx)) . ((x+\sqrtx)/(1-\sqrtx))`
`=(1+\sqrtx-2\sqrtx)/(\sqrtx(1+\sqrtx)) . (\sqrtx(1+\sqrtx))/(1-\sqrtx)`
`=(1-\sqrtx)/(1-\sqrtx)=1`
Câu 2.
a) Với `m=-2`, ta có PT: `x^2-2x-3=0`
Có: `a-b+c=0=> x_1=-1 ; x_2 = 3`
b) PT có 2 nghiệm phân biệt `<=> \Delta' >0`
`<=> 1^2-(m-1)>0`
`<=>m<2`
Theo hệ thức Viet: `x_1+x_2=2`
`x_1x_2=m-1`
Theo đề bài: `x_1^2+x_2^2-3x_1x_2=2m^2+|m-3|`
`<=>(x_1+x_2)^2-5x_1x_2=2m^2-m+3` (Vì `m<2<3`)
`<=> 2^2-5(m-1)=2m^2-m+3`
`<=> -2m^2-4m+6=0`
`<=>`\(\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)
Vậy `m=1;m=-3` thỏa mãn.
8 tháng 6 2021
Câu 5:
`P=((a^2+2b+3)(b^2+3a+3))/((2a+1)(2b+1))`
Áp dụng BĐT cosi ta có:
`a^2+1>=2a`
`=>a^2+2b+3>=2a+2b+2`
Hoàn toàn tương tự:`b^2+2a+3>=2a+2b+2`
`=>((a^2+2b+3)(b^2+3a+3))>=(2a+2b+2)^2`
Áp dụng BĐT cosi:`(x+y)^2>=4xy`
`=>((a^2+2b+3)(b^2+3a+3))>=(2a+2b+2)^2>=4(2a+1)(2b+1)`
`=>P>=(4(2a+1)(2b+1))/((2a+1)(2b+1))`
Dấu "=" xảy ra khi `a=b=1`
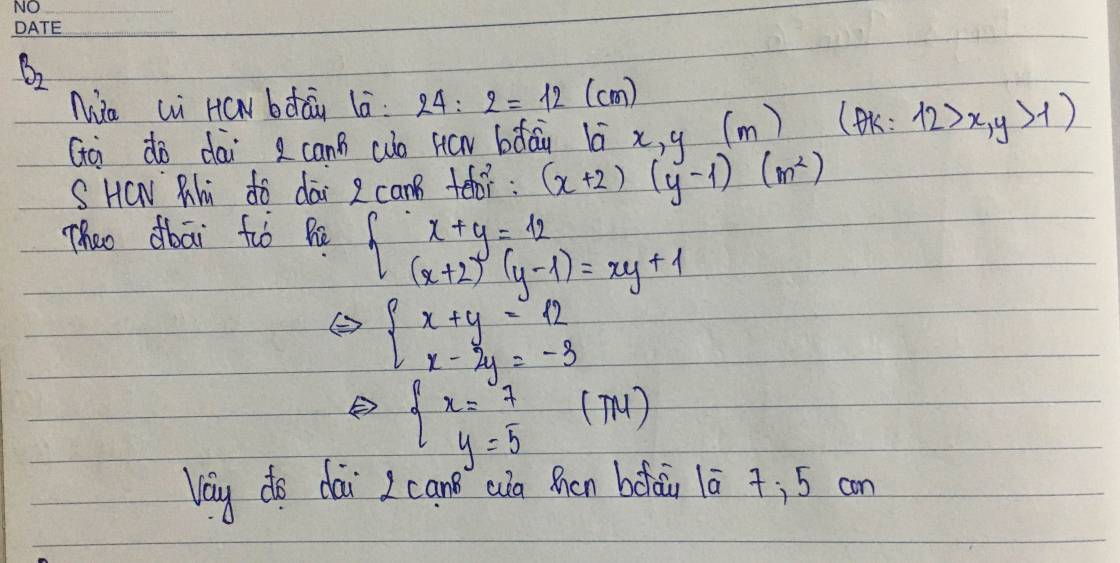
Bài 1 : Với \(x>0;x\ne1\)
a, \(P=\left(\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+1}\right):\left(\frac{1}{\sqrt{x}+1}+\frac{2}{x-1}\right)\)
\(=\left(\frac{x+\sqrt{x}-\sqrt{x}+1}{x-1}\right):\left(\frac{\sqrt{x}-1+2}{x-1}\right)=\frac{x+1}{\sqrt{x}+1}\)
b, Ta có : \(x=4-2\sqrt{3}=\left(\sqrt{3}-1\right)^2\)
Thay vào P ta được : \(\frac{\left(\sqrt{3}-1\right)^2+1}{\sqrt{3}}=\frac{\sqrt{3}\left(\sqrt{3}-1\right)^2+\sqrt{3}}{3}\)
Bài 1.2
\(\hept{\begin{cases}x+2y=6\\2x+3y=7\end{cases}\Leftrightarrow\hept{\begin{cases}2x+4y=12\\2x+3y=7\end{cases}\Leftrightarrow}\hept{\begin{cases}y=5\\x+2y=6\end{cases}}}\)
Thay (1) vào (2)
\(\left(2\right)\Rightarrow x+10=6\Leftrightarrow x=-4\)
Vậy hệ phương trình có một nghiệm ( x ; y ) = ( - 4 ; 5 )